题目内容
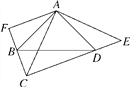
【题目】如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,点D在CE上,AF⊥CB,垂足为F.
(1)若AC=10,求四边形ABCD的面积;
(2)求证:CE=2AF.
【答案】(1) 50;(2)证明见解析.
【解析】(1)求出∠BAC=∠EAD,根据SAS推出△ABC≌△ADE,推出四边形ABCD的面积=三角形ACE的面积,即可得出答案;
(2)过点A作AG⊥CD,垂足为点G,求出AF=AG,进而求出CG=AG=GE,即可得出答案.
(1)∵∠BAD=∠CAE=90°,
∴∠BAC+∠CAD=∠EAD+∠CAD,
∴∠BAC=∠EAD.
在△ABC和△ADE中,
AB=AD,∠BAC=∠DAE,AC=AE,
∴△ABC≌△ADE(SAS).
∴S△ABC=S△ADE,∴S四边形ABCD=S△ABC+S△ACD=S△ADE+S△ACD
=S△ACE=![]() AC·AE=
AC·AE=![]() ×102=50.
×102=50.
(2)∵△ACE是等腰直角三角形,
∴∠ACE=∠AEC=45°.由(1)知△ABC≌△ADE,
∴∠ACB=∠AEC=45°,∴∠ACB=∠ACE,∴CA平分∠ECF.
过点A作AG⊥CD,垂足为点G.
∵AF⊥CB,∴AF=AG.又∵AC=AE,
∴∠CAG=∠EAG=45°,
∴∠CAG=∠EAG=∠ACE=∠AEC,
∴CG=AG=GE,
∴CE=2AG=2AF.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目