题目内容
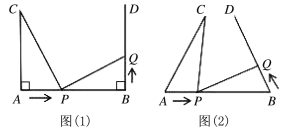
【题目】如图(1),![]() ,
,![]() ,
,![]() 垂足分别为
垂足分别为![]() 、
、![]() ,
,![]() .点
.点![]() 在线段
在线段![]() 上以
上以![]() 的速度由点
的速度由点![]() 向点
向点![]() 运动,同时点
运动,同时点![]() 在射线
在射线![]() 上运动.它们运动的时间为
上运动.它们运动的时间为![]() (当点
(当点![]() 运动结束时,点
运动结束时,点![]() 运动随之结束).
运动随之结束).
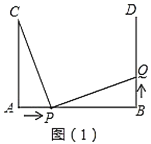
(1)若点![]() 的运动速度与点
的运动速度与点![]() 的运动速度相等,当
的运动速度相等,当![]() 时,
时,![]() 与
与![]() 是否全等,并判断此时线段
是否全等,并判断此时线段![]() 和线段
和线段![]() 的位置关系,请分别说明理由;
的位置关系,请分别说明理由;
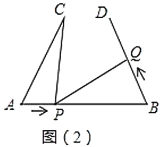
(2)如图(2),若“![]() ,
,![]() ”改为“
”改为“![]() ”,点
”,点![]() 的运动速度为
的运动速度为![]() ,其它条件不变,当点
,其它条件不变,当点![]() 、
、![]() 运动到何处时有
运动到何处时有![]() 与
与![]() 全等,求出相应的
全等,求出相应的![]() 的值.
的值.
【答案】(1)全等,PC⊥PQ,理由见解析;(2)2或![]()
【解析】
(1)利用SAS证得△ACP≌△BPQ,得出∠ACP=∠BPQ,进一步得出∠APC+∠BPQ=∠APC+∠ACP=90°得出结论即可;
(2)由△ACP≌△BPQ,分两种情况:①AC=BP,AP=BQ,②AC=BQ,AP=BP,建立方程组求得答案即可.
解:如图:
(1)△ACP≌△BPQ;
理由:∵AC⊥AB,BD⊥AB
∴∠A=∠B=90°
∵AP=BQ=2,
∴BP=5,
∴BP=AC,
∴△ACP≌△BPQ;
∴∠C=∠BPQ,
∵∠C+∠APC=90°,
∴∠APC+∠BPQ=90°,
∴∠CPQ=90°,
∴PC⊥PQ;
(2)有两种情况;
①若△ACP≌△BPQ,
则AC=BP,AP=BQ,可得:5=7-2t,2t=xt
解得:x=2,t=1;
②若△ACP≌△BQP,
则AC=BQ,AP=BP,可得:5=xt,2t=7-2t
解得:x=![]() ,t=
,t=![]() .
.
综上所述,当△ACP与△BPQ全等时,x的值为2或![]() .
.

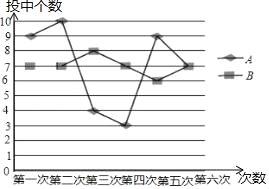
【题目】某班为确定参加学校投篮比赛的任选,在A、B两位投篮高手间进行了6次投篮比赛,每人每次投10个球,将他们每次投中的个数绘制成如图所示的折线统计图.
(1)根据图中所给信息填写下表:
投中个数统计 | 平均数 | 中位数 | 众数 |
A |
| 8 |
|
B | 7 |
| 7 |
(2)如果这个班只能在A、B之间选派一名学生参赛,从投篮稳定性考虑应该选派谁?请你利用学过的统计量对问题进行分析说明.