题目内容
根据下列证明过程填空:
(1)如图,已知直线EF与AB、CD都相交,且AB∥CD,试说明∠1=∠2的理由.
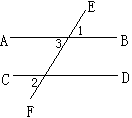
解:∵AB∥CD (已知)
∴∠2=∠3( )
∵∠1=∠3( )
∴∠1=∠2( 等量代换 )
(2)如图,已知:△AOC≌△BOD,试说明AC∥BD成立的理由.
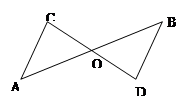
解:∵△AOC≌△BOD
∴∠A= ( )
∴AC∥BD ( )
(1)如图,已知直线EF与AB、CD都相交,且AB∥CD,试说明∠1=∠2的理由.

解:∵AB∥CD (已知)
∴∠2=∠3( )
∵∠1=∠3( )
∴∠1=∠2( 等量代换 )
(2)如图,已知:△AOC≌△BOD,试说明AC∥BD成立的理由.

解:∵△AOC≌△BOD
∴∠A= ( )
∴AC∥BD ( )
(1)两直线平行,同位角相等,对顶角相等;(2)∠B,全等三角形对应角相等,内错角相等,两直线平行
试题分析:根据平行线的性质及全等三角形的性质依次分析即可.
(1)∵AB∥CD (已知)
∴∠2=∠3( 两直线平行,同位角相等 )
∵∠1=∠3( 对顶角相等 )
∴∠1=∠2( 等量代换 ) ;
(2)∵△AOC ≌△BOD
∴∠A= ∠B ( 全等三角形对应角相等 )
∴AC∥BD( 内错角相等 ,两直线平行 )
点评:全等三角形的判定和性质是初中数学的重点,贯穿于整个初中数学的学习,是中考中极为重要的知识点,一般难度不大,需熟练掌握.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目
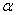 (∠C>∠B),求∠DAE的度数(用含
(∠C>∠B),求∠DAE的度数(用含 。其中能构成直角三角形的有( )组
。其中能构成直角三角形的有( )组 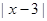 , 一条直角边的长是
, 一条直角边的长是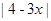 , 那么当另一条直角边达到最大时, 这个直角三角形的周长的范围大致在 ( )
, 那么当另一条直角边达到最大时, 这个直角三角形的周长的范围大致在 ( )

 的值( )
的值( )