题目内容
【题目】在平面直角坐标系xOy中,反比例函数y1= ![]() 的图象与一次函数y2=ax+b的图象交于点A(1,3)和B(﹣3,m).
的图象与一次函数y2=ax+b的图象交于点A(1,3)和B(﹣3,m).
(1)求反比例函数y1= ![]() 和一次函数y2=ax+b的表达式;
和一次函数y2=ax+b的表达式;
(2)点C 是坐标平面内一点,BC∥x 轴,AD⊥BC 交直线BC 于点D,连接AC.若AC= ![]() CD,求点C的坐标.
CD,求点C的坐标.
【答案】
(1)解:∵反比例函数y1= ![]() 的图象与一次函数y2=ax+b的图象交于点A(1,3)和B(﹣3,m),
的图象与一次函数y2=ax+b的图象交于点A(1,3)和B(﹣3,m),
∴点A(1,3)在反比例函数y1= ![]() 的图象上,
的图象上,
∴k=1×3=3,
∴反比例函数的表达式为y1= ![]() .
.
∵点B(﹣3,m)在反比例函数y1= ![]() 的图象上,
的图象上,
∴m= ![]() =﹣1.
=﹣1.
∵点A(1,3)和点B(﹣3,﹣1)在一次函数y2=ax+b的图象上,
∴ ![]() ,解得:
,解得: ![]() .
.
∴一次函数的表达式为y2=x+2.
(2)解:依照题意画出图形,如图所示.
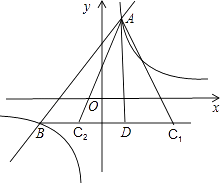
∵BC∥x轴,
∴点C的纵坐标为﹣1,
∵AD⊥BC于点D,
∴∠ADC=90°.
∵点A的坐标为(1,3),
∴点D的坐标为(1,﹣1),
∴AD=4,
∵在Rt△ADC中,AC2=AD2+CD2,且AC= ![]() CD,
CD,
∴ ![]() ,解得:CD=2.
,解得:CD=2.
∴点C1的坐标为(3,﹣1),点C2的坐标为(﹣1,﹣1).
故点C的坐标为(﹣1,﹣1)或(3,﹣1)
【解析】(1)把A点的坐标代入反比例函数解析式可求得k的值可得;再把B点的坐标代入已经求得的反比例函数解析式可求得m的值,再由A、B的坐标和待定系数法求得一次函数的解析式;
(2)易求出C点的纵坐标和点D的坐标,从而可得AD的长;在Rt△ADC中可求得CD的长,从而求出点C的坐标.

【题目】随着我国人口增长速度的减慢,小学入学儿童数量有所减少.下表中的数据近似地呈现了某地区入学儿童人数的变化趋势:
年份 | 2015 | 2016 | 2017 | … |
入学儿童人数 | 2520 | 2330 | 2140 | … |
(1)上表中_____是自变量,_____是因变量;
(2)你预计该地区从_____年起入学儿童的人数不超过2000人.