题目内容
【题目】已知:关于x的二次函数y=x2+bx+c经过点(﹣1,0)和(2,6).
(1)求b和c的值.
(2)若点A(n,y1),B(n+1,y2),C(n+2,y3)都在这个二次函数的图象上,问是否存在整数n,使 ![]() +
+ ![]() +
+ ![]() =
= ![]() ?若存在,请求出n;若不存在,请说明理由.
?若存在,请求出n;若不存在,请说明理由.
(3)若点P是二次函数图象在y轴左侧部分上的一个动点,将直线y=﹣2x沿y轴向下平移,分别交x轴、y轴于C、D两点,若以CD为直角边的△PCD与△OCD相似,请求出所有符合条件点P的坐标.
【答案】
(1)解:把(﹣1,0)和(2,6)代入y=x2+bx+c中,
得 ![]() 解得
解得 ![]() ,
,
∴b=1,c=0.
(2)解:由题意y1=n2+n,y2=(n+1)2+(n+1),y3=(n+2)2+(n+2),
∵ ![]() +
+ ![]() +
+ ![]() =
= ![]() ,
,
∴ ![]() +
+ ![]() +
+ ![]() =
= ![]() ,
,
∴ ![]() ﹣
﹣ ![]() +
+ ![]() ﹣
﹣ ![]() +
+ ![]() ﹣
﹣ ![]() =
= ![]() ,
,
∴ ![]() ﹣
﹣ ![]() =
= ![]() ,
,
整理得n2+3n﹣10=0,
解得n=2或﹣5.
经过检验n=2和﹣5是分式方程的解.
(3)解:当D为直角顶点时,由图象可知不存在点P,使得△PCD为直角三角形,当C为直角顶点,CD为直角边时,作PE⊥OC于E.

设直线y=﹣2x向下平移m个单位,则直线CD解析式为y=﹣2x﹣m,
∴点D坐标(0,﹣m),点C坐标(﹣ ![]() ,0),
,0),
∴OD=m,OC= ![]() ,
,
∴OD=20C,
∵△PCD与△OCD相似,
∴CD=2PC或PC=2CD,
①当CD=2PC时,
∵∠PCD=90°,
∴∠PCE+∠DCO=90°,∠DCO+∠CDO=90°,
∴∠PCE=∠CDO,
∵∠PEC=∠COD=90°,
∴△COD∽△PEC,
∴ ![]() =
= ![]() =
= ![]() =2,
=2,
∴EC= ![]() ,PE=
,PE= ![]() ,
,
∴点P坐标(﹣m,﹣ ![]() ),代入y=x2+x,
),代入y=x2+x,
得﹣ ![]() =m2﹣m,解得m=
=m2﹣m,解得m= ![]() 或(0舍弃)
或(0舍弃)
∴点P坐标(﹣ ![]() ,﹣
,﹣ ![]() ).
).
②PC=2CD时,由 ![]() =
= ![]() =
= ![]() =
= ![]() ,
,
∴EC=2m,PE=m,
∴点P坐标(﹣ ![]() m,﹣m),代入y=x2+x,
m,﹣m),代入y=x2+x,
得﹣m= ![]() m2﹣
m2﹣ ![]() m,
m,
解得m= ![]() 和(0舍弃),
和(0舍弃),
∴点P坐标(﹣ ![]() ,﹣
,﹣ ![]() ).
).
【解析】(1)利用待定系数法求得抛物线的解析式即可得;
(2)直接把A、B、C三点的坐标代入(1)中所求得解析式可得y1,y2,y3的值,再代入所给的得y1,y2,y3之间的关系式化简解方程可得;
(3)分D、C分别为直角顶点来讨论求解.注意C为直角顶点存在两种情况:CD=2PC和PC=2CD.
【考点精析】解答此题的关键在于理解去分母法的相关知识,掌握先约后乘公分母,整式方程转化出.特殊情况可换元,去掉分母是出路.求得解后要验根,原留增舍别含糊,以及对二次函数图象的平移的理解,了解平移步骤:(1)配方 y=a(x-h)2+k,确定顶点(h,k)(2)对x轴左加右减;对y轴上加下减.

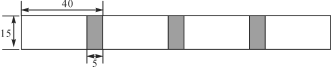
【题目】将长为40 cm、宽为15 cm的长方形白纸,按如图所示的方法黏合起来,黏合部分宽为5 cm.
 …
…
(1)根据上图,将表格补充完整:
白纸张数 | 1 | 2 | 3 | 4 | 5 | … |
纸条长度 | 40 | 110 | 145 | … |
(2)设x张白纸黏合后的总长度为y cm,则y与x之间的关系式是什么?
(3)你认为多少张白纸黏合起来总长度可能为2 018 cm吗?为什么?