题目内容
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交与
轴分别交与![]() 、
、![]() 两点,
两点,![]() .
.
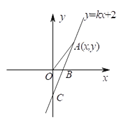
(![]() )写出
)写出![]() 点的坐标和
点的坐标和![]() 的值.
的值.
(![]() )若点
)若点![]() 是第一象限内的直线
是第一象限内的直线![]() 上的一个动点,当点
上的一个动点,当点![]() 运动过程中,试求出
运动过程中,试求出![]() 的面积
的面积![]() 与
与![]() 的函数关系式.
的函数关系式.
(![]() )在(
)在(![]() )的条件下:
)的条件下:
①当点![]() 运动到什么位置时,
运动到什么位置时,![]() 的面积是
的面积是![]() .
.
②在①成立的情况下,![]() 轴上是否存在一点
轴上是否存在一点![]() ,使
,使![]() 是等腰三角形.若存在,请写出满足条件的所有
是等腰三角形.若存在,请写出满足条件的所有![]() 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
【答案】(![]() )
)![]() ,
,![]() ;(
;(![]() )
)![]() ;(
;(![]() )①当
)①当![]() 时,
时,![]() 的面积为
的面积为![]() .②
.②![]() ,
,![]() ,
,![]() ,
,![]()
【解析】试题分析:(1)对于直线解析式,分别令x与y为0求出对应y与x的值,表示出OB与OC,根据已知等式确定出k的值,即可求出B的坐标;
(2)过A作AD垂直于x轴,可得AD为三角形AOB的高,根据三角形面积公式列出S与x的关系式即可;
(3)①令S=2,求出x的值,确定出A的坐标即可;
②在①成立的情况下,x轴上存在一点P,使△POA是等腰三角形,如图所示,分别求出P的坐标即可.
试题解析:
(![]() )令
)令![]() 中
中![]() ,
,
则![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,
代入得![]() ,
,![]() .
.
(![]() )作
)作![]() 轴于
轴于![]()
∴![]() .
.
∵![]() 轴,
轴,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
(![]() )①由已知可得
)①由已知可得![]() ,
,
![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴当![]() 时,
时,![]() 的面积是
的面积是![]() .
.
②∵![]()
∴![]() .
.
∵![]() 为等腰
为等腰![]() .
.
若![]() ,则以
,则以![]() 为圆心,
为圆心,![]() 为半径画圆,交
为半径画圆,交![]() 轴于
轴于![]() ,
,
∴![]() ,
,
若![]() ,则以
,则以![]() 为圆心,
为圆心,![]() 为半径画圆,交
为半径画圆,交![]() 轴于
轴于![]() ,
,![]() ,
,
∴![]() ,
,![]()
若![]() ,则作
,则作![]() 的垂直平分线,交
的垂直平分线,交![]() 轴于
轴于![]() ,
,
∴![]() .
.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目