题目内容
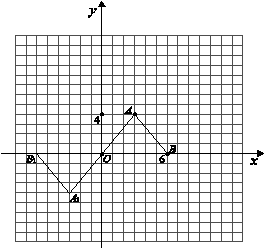
如图，正方形ABCD在平面直角坐标系中的位置如图所示，点B与原点重合，点D坐标为（4，4），当三角板直角顶点P坐标为（
）时，设一直角边与x轴交于点E，另一直角边与y轴交于点F，在三角板绕点P旋转的过程中，使得△POE能否成为等腰三角形．请写出所有满足条件的点F的坐标 。
）时，设一直角边与x轴交于点E，另一直角边与y轴交于点F，在三角板绕点P旋转的过程中，使得△POE能否成为等腰三角形．请写出所有满足条件的点F的坐标 。
，
，
，
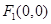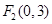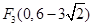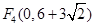
试题分析：使△POE是等腰三角形的条件是：OP、PE、EO其中两段相等，P（3，3），那么有：
①PE⊥OC和F点过（0，0）点，PE=OE，则F点是（0，3）和（0，0）；∵P坐标为（3，3），∴OP=
，②PE⊥OP和F点过（0，6- ），则PE=OP，则F点是（0，6+）和（0，6-）点评：该题主要考查学生对等腰三角形的概念的理解，以及在直角坐标系中如何表示，建议学生结合画图解决该种题目。
练习册系列答案
阅读快车系列答案
相关题目
(
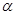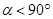)，在旋转过程中：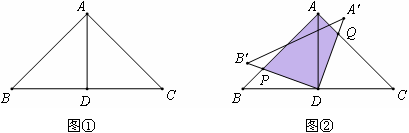
，那么
等于 （ ）
