Question

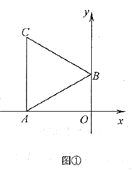
【题目】在平面中，给定线段AB和C，P两点，点C与点P分布在线段AB的异侧，满足，则称点C与点P是关于线段AB的关联点．在平面直角坐标系xOy中，已知点，，．

（1）在，，三个点中，点O与点P是关于线段AB的关联点的是________；

（2）若点C与点P是关于线段OA的关联点，求点P的纵坐标m的取值范围；

（3）直线与x轴，y轴分别交与点E，F，若在线段AB上存在点P与点O是关于线段EF的关联点，直接写出b的取值范围．

Answer 1

【答案】（1）P1， P3；（2）-≤m<0；（3）1≤b<2

【解析】

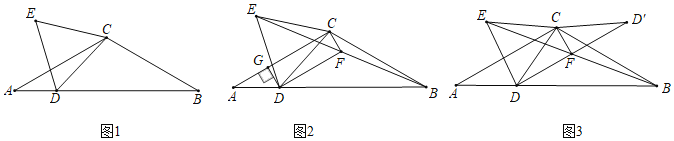
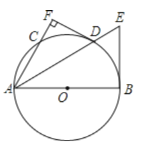
（1）分别求出∠AP1B，∠AP2B，∠AP3B，当所求角等于90°时即为点O的关联点；

（2）根据题意确定点O、A、C、P四边共圆，故点P在劣弧OA上，当CP是直径时，存在m的最小值，利用勾股定理求出半径AE，即可得到PD，由此求出m的最小值，得到m的取值范围；

（3）求出直线AB的解析式为y=-x+2，证明直线与直线AB平行，当以EF为直径的圆与直线AB相切时有最小值，与直线AB相交时都可得到∠EPF=90°，故b<2，求出以EF为直径的圆与直线AB相切时FP=OF=BF=1，由此得到b的取值范围．

解：(1)∵，，

∴,

∵,

∴， ,

∴，

∴∠AP1B=90°，

∴∠AOB+∠AP1B=180°，

∴点O与点P1是关于线段AB的关联点；

∵，

∴，

∴,

∴，故点O与点P2不是关于线段AB的关联点；

∵，

∴，

∴，

∴，

∴∠AOB+∠AP3B=180°，

∴点O与点P3是关于线段AB的关联点；

故答案为：P1、P3；

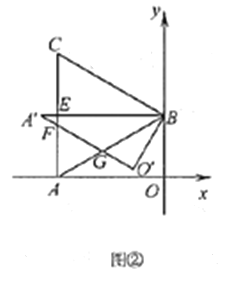
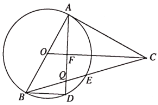
(2) ∵点C与点P是关于线段OA的关联点，

∴点O、A、C、P四边共圆，故点P在劣弧OA上，当CP是直径时，存在m的最小值，

设圆心为E，

∵,A（2,0），

∴CP⊥OA，CD=，OD=AD=1，

∵,

∴,

∴,

∴,

∴PD=,即m=-，

∴-≤m<0 ；

(3)设直线AB的解析式为y=mx+n，将点A(2,0)，B(0，2)代入，得

，∴，

∴直线AB的解析式为y=-x+2，

∴直线与直线AB平行，

∵A(2,0)，B(0，2),

∴OA=OB，

∴∠OFE=∠OBA=45°，

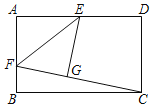
∵∠EOF=90°，点P与点O是关于线段EF的关联点，

∴∠EPF=90°，

∴当以EF为直径的圆与直线AB相切时有最小值，与直线AB相交时都可得到∠EPF=90°，故b<2，

当以EF为直径的圆与直线AB相切时，连接EF中点N与点P，连接PE、PF，

∴∠BPN=90°，

∴∠FNP=90°，

∵FN=PN，

∴∠NFP=∠NPF=45°，

∴∠OFP=90°，

∴四边形OFPE是矩形，

∵OF=OE，

∴四边形OFPE是正方形，

∴OF=PF=BF=1，

∴1≤b<2．