题目内容
【题目】在等边△ABC外作射线AD,使得AD和AC在直线AB的两侧,∠BAD=α(0°<α<180°),点B关于直线AD的对称点为P,连接PB,PC.
(1)依题意补全图1;
(2)在图1中,求△BPC的度数;
(3)直接写出使得△PBC是等腰三角形的α的值.

【答案】(1)详见解析;(2)∠BPC=30°;(3)α的值为:30°,75°,120°,165°.
【解析】
(1)根据题意画出图形即可;
(2)点B关于直线AD的对称点为P,得到AP=AB,根据圆周角定理即可解决问题;
(3)根据等腰三角形的性质分四种情形画出图形分别求解即可.
(1)图形如图所示:
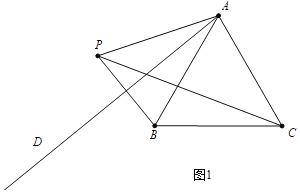
(2)点B关于直线AD的对称点为P,
∴AP=AB,
∴∠PAD=∠BAD,
∵△ABC是等边三角形,
∴∠BAC=60°,AB=AC,
∴AP=AB=AC,
∴P,B,C在以A为圆心AP为半径的圆上,
∴∠BPC=![]() ∠BAC=30°;
∠BAC=30°;
(3)①如图2-1中,当BP=BC时,α=∠BAD=30°.
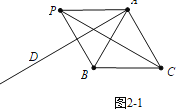
②如图2-2中,当PB=PC时,α=∠BAD=75°.

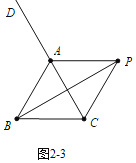
③如图2-3中,当CP=BC时,α=∠BAD=120°
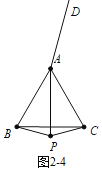
④如图2-4中,当BP=PC时,α=∠BAD=165°
综上所述α的值为:30°,75°,120°,165°.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目