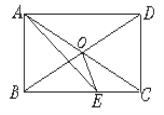
题目内容
【题目】如图,矩形ABCD的对角线AC,BD相交于点O,点E,F,M,N分别为OA,OB,OC,OD的中点,连接EF,FM,MN,NE.
(1)依题意,补全图形;
(2)求证:四边形EFMN是矩形;
(3)连接DM,若DM⊥AC于点M,ON=3,求矩形ABCD的面积.
【答案】(1)补图见解析;(2)证明见解析;(3) 36![]()
【解析】试题分析:(1)见图形;(2)根据三角形的中位线定理,先证四边形EFMN是平行四边形,再通过对角线相等证明四边形EFMN是矩形;(3)证△OCD是等边三角形。
试题解析:(1)解:如图所示:
(2)证明:∵点E,F分别为OA,OB的中点,∴EF∥AB,EF=![]() AB,
AB,
同理:NM∥CD,MN=![]() DC,∵四边形ABCD是矩形,∴AB∥DC,AB=DC,AC=BD,
DC,∵四边形ABCD是矩形,∴AB∥DC,AB=DC,AC=BD,
∴EF∥NM,EF=MN,∴四边形EFMN是平行四边形,
∵点E,F,M,N分别为OA,OB,OC,OD的中点,∴EO=![]() AO,MO=
AO,MO=![]() CO,
CO,
在矩形ABCD中,AO=CO=![]() AC,BO=DO=
AC,BO=DO=![]() BD,∴EM=EO+MO=
BD,∴EM=EO+MO=![]() AC,
AC,
 同理可证FN=
同理可证FN=![]() BD,∴EM=FN,∴四边形EFMN是矩形.
BD,∴EM=FN,∴四边形EFMN是矩形.
(3)解:∵DM⊥AC于点M,由(2)MO=![]() CO,∴DO=CD,
CO,∴DO=CD,
在矩形ABCD中,AO=CO=![]() AC,BO=DO=
AC,BO=DO=![]() BD,AC=BD,
BD,AC=BD,
∴AO=BO=CO=DO,∴△COD是等边三角形,∴∠ODC=60°,∵MN∥DC,
∴∠FNM=∠ODC=60°,在矩形EFMN中,∠FMN=90°.∴∠NFM=90°﹣∠FNM=30°,
∵NO=3,∴FN=2NO=6,FM=3![]() ,MN=3,∵点F,M分别为OB,OC的中点,
,MN=3,∵点F,M分别为OB,OC的中点,
∴BC=2FM=6![]() ,∴矩形的面积为BCCD=36
,∴矩形的面积为BCCD=36![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】为了让同学们了解自己的体育水平,初二1班的体育康老师对全班45名学生进行了一次体育模拟测试(得分均为整数)成绩满分为10分,成绩达到9分以上(包含9分)为优秀,成绩达到6分以上(包含6分)为合格,1班的体育委员根据这次测试成绩,制作了统计图和分析表如下:
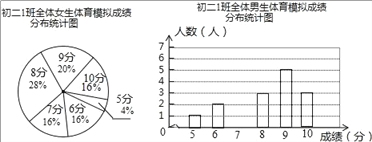
初二1班体育模拟测试成绩分析表
平均分 | 方差 | 中位数 | 众数 | 合格率 | 优秀率 | |
男生 | 2 | 8 | 7 | 95% | 40% | |
女生 | 7.92 | 1.99 | 8 | 96% | 36% |
根据以上信息,解答下列问题:
(1)在这次测试中,该班女生得10分的人数为4人,则这个班共有女生______人;
(2)补全初二1班男生体育模拟测试成绩统计图,并把相应的数据标注在统计图上;
(3)补全初二1班体育模拟测试成绩分析表;
(4)你认为在这次体育测试中,1班的男生队、女生队哪个表现更突出一些?并写出一条支持你的看法的理由;
(5)体育康老师说,从整体看,1班的体育成绩在合格率方面基本达标,但在优秀率方面还不够理想,因此他希望全班同学继续加强体育锻炼,争取在期末考试中,全班的优秀率达到60%,若男生优秀人数再增加6人,则女生优秀人数再增加多少人才能完成康老师提出的目标?