ЬтФПФкШн
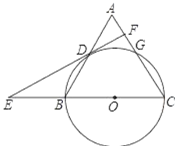
ЁОЬтФПЁПФГОАЧјЕФШ§ИіОАЕуAЃЌBЃЌCдкЭЌвЛЯпТЗЩЯЃЎМзЁЂввСНУћгЮПЭДгОАЕуAГіЗЂЃЌМзВНааЕНОАЕуCЃЛввЯШГЫОАЧјЙлЙтГЕЕНОАЕуBЃЌдкBДІЭЃСєвЛЖЮЪБМфКѓЃЌдйВНааЕНОАЕуCЃЌМзЁЂввСНШЫЭЌЪБЕНДяОАЕуCЃЎМзЁЂввСНШЫОрОАЕуAЕФТЗГЬy(Уз)гыМзГіЗЂЕФЪБМфx(Зж)жЎМфЕФКЏЪ§ЭМЯѓШчЭМЫљЪОЃК
(1)МзВНааЕФЫйЖШЮЊ_____Уз/ЗжЃЌввВНааЪБЕФЫйЖШЮЊ_____Уз/ЗжЃЛ
(2)ЧѓввГЫОАЧјЙлЙтГЕЪБyгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
(3)ЮЪМзГіЗЂЖрГЄЪБМфгыввдкЭОжаЯргіЃЌЧыжБНгаДГіНсЙћЃЎ
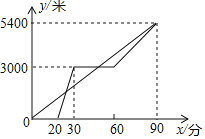
ЁОД№АИЁП(1)60ЃЌ80ЃЛ(2)yЃН300xЉ6000(20ЁмxЁм30)ЃЛ(3)МзГіЗЂ25ЗжжгКЭ50ЗжжггыввСНДЮдкЭОжаЯргіЃЎ
ЁОНтЮіЁП
(1)гЩЭМЯѓЕУЯргІЕФТЗГЬКЭЪБМфЃЌРћгУТЗГЬГ§вдЪБМфЕУЫйЖШЃЛ
(2)ЩшввГЫОАЧјЙлЙтГЕЪБyгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЮЊyЃНkx+b(kЁй0)ЃЌНЋ(20ЃЌ0)ЃЌ(30ЃЌ3000)ДњШыЃЌЧѓГіkКЭbЕФжЕдйДњЛиМДПЩЃЛ
(3)ЯШЧѓГіМзЕФКЏЪ§НтЮіЪНЃЌдйНЋЦфгыввГЫЙлЙтГЕЪБЕФНтЮіЪНСЊСЂЕУЕквЛДЮЯргіЪБМфЃЛдкМзЕФНтЮіЪНжаЃЌСюyЃН3000ЃЌЧѓЕУЕкЖўДЮЯргіЪБМфЃЎ
(1)МзВНааЕФЫйЖШЮЊЃК5400ЁТ90ЃН60(Уз/Зж)ЃЛ
ввВНааЕФЫйЖШЮЊЃК(5400Љ3000)ЁТ(90Љ60)ЃН80(Уз/Зж)ЃЎ
ЙЪД№АИЮЊЃК60ЃЌ80ЃЛ
(2)НтЃКИљОнЬтвтЃЌЩшввГЫОАЧјЙлЙтГЕЪБyгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЮЊyЃНkx+b(kЁй0)ЃЌНЋ(20ЃЌ0)ЃЌ(30ЃЌ3000)ДњШыЕУЃК
![]() НтЕУЃК
НтЕУЃК![]() ЃЎ
ЃЎ
ЁрввГЫОАЧјЙлЙтГЕЪБyгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЮЊyЃН300xЉ6000(20ЁмxЁм30)
(3)ЩшМзЕФКЏЪ§НтЮіЪНЮЊЃКyЃНkxЃЌНЋ(90ЃЌ5400)ДњШыЕУkЃН60ЃЌ
ЁрyЃН60xЃЎ
гЩ![]() ЕУxЃН25ЃЌМДМзГіЗЂ25ЗжжггыввЕквЛДЮЯргіЃЛ
ЕУxЃН25ЃЌМДМзГіЗЂ25ЗжжггыввЕквЛДЮЯргіЃЛ
дкyЃН60xжаЃЌСюyЃН3000ЕУЃКxЃН50ЃЌДЫЪБМзгыввЕкЖўДЮЯргіЃЎ
МзГіЗЂ25ЗжжгКЭ50ЗжжггыввСНДЮдкЭОжаЯргіЃЎ

ЁОЬтФПЁПОХЃЈ1ЃЉАрЪ§бЇаЫШЄаЁзщОЙ§ЪаГЁЕїВщЃЌећРэГіФГжжЩЬЦЗдкЕкxЃЈ1ЁмxЁм90ЃЉЬьЕФЪлМлгыЯњЪлСПЕФЯрЙиаХЯЂШчЯТБэЃК
ЪБМфxЃЈЬьЃЉ | 1ЁмxЃМ50 | 50ЁмxЁм90 |
ЪлМлЃЈдЊ/МўЃЉ | xЃЋ40 | 90 |
УПЬьЯњСПЃЈМўЃЉ | 200Ѓ2x | |
вбжЊИУЩЬЦЗЕФНјМлЮЊУПМў30дЊЃЌЩшЯњЪлИУЩЬЦЗЕФУПЬьРћШѓЮЊyдЊ[
ЃЈ1ЃЉЧѓГіyгыxЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉЮЪЯњЪлИУЩЬЦЗЕкМИЬьЪБЃЌЕБЬьЯњЪлРћШѓзюДѓЃЌзюДѓРћШѓЪЧЖрЩйЃП
ЃЈ3ЃЉИУЩЬЦЗдкЯњЪлЙ§ГЬжаЃЌЙВгаЖрЩйЬьУПЬьЯњЪлРћШѓВЛЕЭгк4800дЊЃПЧыжБНгаДГіНсЙћ.
ЁОЬтФПЁПжаЛЊЮФУїЃЌдДдЖСїГЄЃЛжаЛЊККзжЃЌдЂвтЩюЙуЃЎЮЊДЋГажаЛЊгХауДЋЭГЮФЛЏЃЌФГаЃЭХЮЏзщжЏСЫвЛДЮШЋаЃ3000УћбЇЩњВЮМгЕФЁАККзжЬ§аДЁБДѓШќЃЎЮЊСЫНтБОДЮДѓШќЕФГЩМЈЃЌаЃЭХЮЏЫцЛњГщШЁСЫЦфжа200УћбЇЩњЕФГЩМЈзїЮЊбљБОНјааЭГМЦЃЌжЦГЩШчЯТВЛЭъећЕФЭГМЦЭМБэЃК
ЦЕЪ§ЦЕТЪЗжВМБэ
ГЩМЈxЃЈЗжЃЉ | ЦЕЪ§ЃЈШЫЃЉ | ЦЕТЪ |
50ЁмxЃМ60 | 10 | 0.05 |
60ЁмxЃМ70 | 30 | 0.15 |
70ЁмxЃМ80 | 40 | n |
80ЁмxЃМ90 | m | 0.35 |
90ЁмxЁм100 | 50 | 0.25 |
ИљОнЫљИјаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉm=ЁЁ ЁЁЃЌn=ЁЁ ЁЁЃЛ
ЃЈ2ЃЉВЙШЋЦЕЪ§ЗжВМжБЗНЭМЃЛ
ЃЈ3ЃЉет200УћбЇЩњГЩМЈЕФжаЮЛЪ§ЛсТфдкЁЁ ЁЁЗжЪ§ЖЮЃЛ
ЃЈ4ЃЉШєГЩМЈдк90ЗжвдЩЯЃЈАќРЈ90ЗжЃЉЮЊЁАгХЁБЕШЃЌЧыФуЙРМЦИУаЃВЮМгБОДЮБШШќЕФ3000УћбЇЩњжаГЩМЈЪЧЁАгХЁБЕШЕФдМгаЖрЩйШЫЃП