题目内容
【题目】已知∠AOB=70°,∠AOD=![]() ∠AOC,∠BOD=3∠BOC(∠BOC<45°),则∠BOC的度数是______.
∠AOC,∠BOD=3∠BOC(∠BOC<45°),则∠BOC的度数是______.
【答案】10°或14°或30°或42°
【解析】
①当射线OC在∠AOB内部时,此时射线OD的位置只有两种可能:i)若射线OD在∠AOC内部,ii)若射线OD在∠AOB外部,
②当射线OD在∠AOB外部时,i)若射线DO在∠AOB内部,ii)若射线OD在∠AOB外部分别求出即可.
解:设∠BOC=α,
∴∠BOD=3∠BOC=3α,
依据题意,分两种情况:
①当射线OC在∠AOB内部时,此时射线OD的位置只有两种可能:
i)若射线OD在∠AOC内部,如图2,
∴∠COD=∠BOD-∠BOC=2α,
∵∠AOD=![]() ∠AOC,
∠AOC,
∴∠AOD=∠COD=2α,
∴∠AOB=∠AOD+∠BOD=2α+3α=5α=70°,
∴α=14°,
∴∠BOC=14°;
ii)若射线OD在∠AOB外部,如图3,
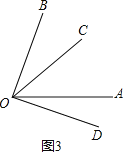
∴∠COD=∠BOD-∠BOC=2α,
∵∠AOD=![]() ∠AOC,
∠AOC,
∴∠AOD=![]() ∠COD=
∠COD=![]() α,
α,
∴∠AOB=∠BOD-∠AOD=3α-![]() α=
α=![]() α=70°,
α=70°,
∴α=30°,
∴∠BOC=30°;
②当射线OD在∠AOB外部时,
依据题意,此时射线OC靠近射线OB,
∵∠BOC<45°,∠AOD=![]() ∠AOC,
∠AOC,
∴射线OD的位置也只有两种可能:
i)若射线DO在∠AOB内部,如图4,
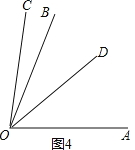
则∠COD=∠BOC+∠BOD=4α,
∵∠AOD=![]() ∠AOC,
∠AOC,
∴∠AOD=∠COD=4α,
∴∠AOB=∠BOD+∠AOD=4α,
∴AOB=∠BOD+∠AOD=3α+4α=7α=70°,
∴α=10°,
∴∠BOC=10°
ii)若射线OD在∠AOB外部,如图5,

则∠COD=∠BOC+∠DOB=4α,
∵∠AOD=![]() ∠AOC,
∠AOC,
∴∠AOD=![]() ∠COD=
∠COD=![]() α,
α,
∴∠AOB=∠BOD-∠AOD=3α-![]() α=
α=![]() α=70°,
α=70°,
∴α=42°,
∴∠BOC=42°,
综上所述:∠BOC的度数分别是10°,14°,30°,42°.
故答案为:10°或14°或30°或42°