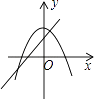��Ŀ����
����Ŀ������ѧ���о����֣�һ������£�һ�ڿ�40�����У�ѧ����ע�������ʦ���εı仯���仯����ʼ�Ͽ�ʱ��ѧ����ע��������ǿ���м���һ��ʱ��ѧ����ע�������ֽ�Ϊ������ȶ�״̬�����ѧ����ע������ʼ��ɢ������ʵ�������֪��ѧ����ע����ָ����y��ʱ��x�����ӣ��ı仯��������ͼ��ʾ������AB��BC�ֱ�Ϊ�߶Σ�CDΪ˫���ߵ�һ���֣���
��1����ʼ�Ͽκ�������ʱ�����ʮ����ʱ��Ƚϣ���ʱѧ����ע���������У�
��2��һ����ѧ�����⣬��Ҫ��19���ӣ�Ϊ��Ч���Ϻã�Ҫ��ѧ����ע����ָ������ʹﵽ36����ô�����ʵ����ţ���ʦ�ܷ���ѧ��ע�����ﵽ�����״̬�½����������Ŀ��
���𰸡�
��1���⣺���߶�AB���ڵ�ֱ�ߵĽ���ʽΪy1=k1x+20��
��B��10��40������ã�k1=2��
��y1=2x+20��
��C��D����˫���ߵĽ���ʽΪy2= ![]() ��
��
��C��25��40������ã�k2=1000��
�� ![]()
��x1=5ʱ��y1=2��5+20=30��
�� ![]() ��
��
��y1��y2
���30����ע���������У�
��2���⣺��y1=36��
��36=2x+20��
��x1=8
��y2=36��
�� ![]() ��
��
�� ![]()
��27.8��8=19.8��19��
�ྭ���ʵ����ţ���ʦ����ѧ��ע�����ﵽ�����״̬�½����������Ŀ��
����������1������һ�κ����ͷ�����������Ӧ�ã��ô���ϵ��������߶�AB���ڵ�ֱ�ߵĽ���ʽ����C��D����˫���ߵĽ���ʽ����x1=5ʱ�� ![]() ���бȽϵõ�y1��y2���ó���30����ע���������У���2����y1=36ʱ���õ�x1=8����y2=36���õ�
���бȽϵõ�y1��y2���ó���30����ע���������У���2����y1=36ʱ���õ�x1=8����y2=36���õ� ![]() ����27.8��8=19.8��19�����Ծ����ʵ����ţ���ʦ����ѧ��ע�����ﵽ�����״̬�½����������Ŀ.
����27.8��8=19.8��19�����Ծ����ʵ����ţ���ʦ����ѧ��ע�����ﵽ�����״̬�½����������Ŀ.