题目内容
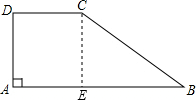
已知：如图，在四边形ABCD中，AB∥CD，∠A=90°，CD=6，AB=15，tan∠B=
．求：BC的长．
| 2 |
| 3 |
过点C作CE⊥AB交AB于E，
∵AB∥CD，∠A=90°
∴∠D=90°
∴四边形AECD是矩形．
∴AE=DC=6．
∵AB=15，
∴BE=9．
在Rt△BEC中，
∵tan∠B=
，BE=9．
∴CE=6．
由勾股定理，得BC=
=3
．
∵AB∥CD，∠A=90°
∴∠D=90°
∴四边形AECD是矩形．
∴AE=DC=6．
∵AB=15，
∴BE=9．
在Rt△BEC中，
∵tan∠B=
| 2 |
| 3 |
∴CE=6．
由勾股定理，得BC=
| BE2+CE2 |
| 13 |
练习册系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
