题目内容
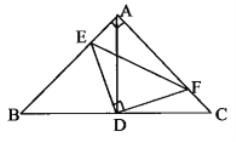
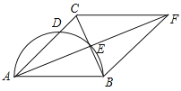
【题目】如图, 已知等边![]() , 点
, 点![]() 在射线
在射线![]() 上(不与
上(不与![]() 重合),连接
重合),连接![]() , 将射线
, 将射线![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 交射线
交射线![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 交直线
交直线![]() 于点
于点![]() .
.
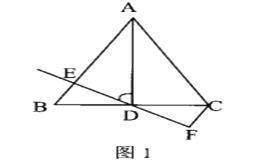
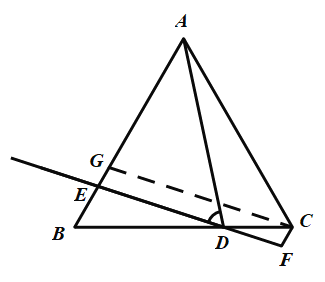
(1)如图1,当点D为线段BC中点时,请直接写出CF,BE,CD三条线段之间的数量;
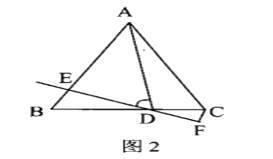
(2)如图2,“点![]() 在线段
在线段![]() 上且不是
上且不是![]() 中点时,
中点时,![]() 中结论是否成立?若成立,请说明理由。若不成立,请写出正确的结论并说明理由;
中结论是否成立?若成立,请说明理由。若不成立,请写出正确的结论并说明理由;
(3)若![]() ,当
,当![]() 时,请直接写出线段
时,请直接写出线段![]() 的长.
的长.
【答案】(1)![]() (2)成立,理由见解析(3)
(2)成立,理由见解析(3)![]() 或
或![]() 或
或![]()
【解析】
(1)由CF∥AB,点D为线段BC中点可得△BDE≌△CDF,根据射线![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,推出∠CDF=30°,CF=
,推出∠CDF=30°,CF=![]() CD即可得出结论;
CD即可得出结论;
(2)作CG∥EF,可得四边形![]() 是平行四边形,根据平行线的性质和等边三角形的性质可推出△BCG≌△CAD即可得出结论;
是平行四边形,根据平行线的性质和等边三角形的性质可推出△BCG≌△CAD即可得出结论;
(3)分点D在线段BC上和点D在BC的延长线上两种情况进行讨论,根据△BDE∽△CDF,对应边成比例即可求出答案.
(1)![]() ,
,
证明:∵△ABC是等边三角形,点D为线段BC中点,
∴∠ADB=90°,BD=CD,
∵CF∥AB,
∴∠DBE=∠DCF,
∵∠BDE=∠CDF
∴△BDE≌△CDF,
∴BE=CF,
∵射线![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,
,
∴∠ADE=60°,
∴∠BDE=∠CDF=30°,
∴CF=![]() CD
CD
∴CF+BE=CD;
(2)成立
理由:作CG∥EF,交AB于点G,如图,
∵![]()
![]() 四边形
四边形![]() 是平行四边形
是平行四边形
![]() ,
,![]()
∵![]() 是等边三角形
是等边三角形
![]() ,
,![]()
又∵![]() ,
,
![]()
![]()
∵![]()
![]()
![]()
∴△BCG≌△CAD,
![]()
∵![]()
![]() ;
;
(3)当点D在线段BC上,
设CF=x,则EG=x,
∵CF∥AB,
∴△BDE∽△CDF,
∴![]() ,
,
∴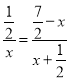 ,
,
∴![]() ,
,![]() ,
,

当点D在BC的延长线上,如图,
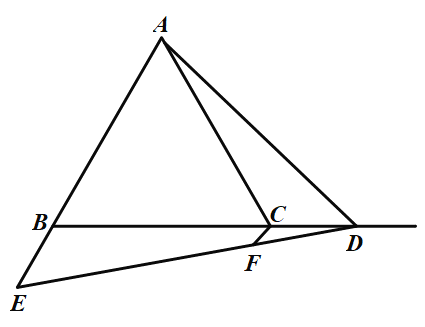
同理可得:△BCG≌△CAD,
∴BE-CF=CD,
设CF=x,则CD=![]() ,
,
∵CF∥AB,
∴△BDE∽△CDF,
∴![]() ,
,
∴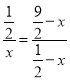 ,解得:
,解得:
![]() ,
,![]() (舍去),
(舍去),
综上所述,CF的长为:![]() 或
或![]() 或
或![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】某社区招募了40位居民参加“众志成城,抗击疫情”志愿者服务活动,对志愿者一天的服务时长进行调查,由调查结果绘制了如下不完整的频数分布表和扇形统计图.
频数分布表
组别 | 时间/小时 | 频数/人数 |
A组 | 0≤ | 2 |
B组 | 1≤ | m |
C组 | 2≤ | 10 |
D组 | 3≤ | 12 |
E组 | 4≤ | 7 |
F组 |
| 4 |
扇形统计图
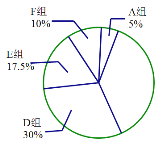
请根据图表中的信息解答下列问题:
(1)求频数分布表中的![]() 的值;
的值;
(2)求B组,C组在扇形统计图中分别对应扇形的圆心角的度数,并补全扇形统计图;
(3)已知F组的志愿者中,只有1名女志愿者.要从该组中选取两名志愿者分发生活物资,请用树状图或列表的方法求2名志愿恰好都是男士的概率.