题目内容
如图,直线l1,l2分别交x轴A、D两点,交y轴于B、C两点,若△AOB≌△COD,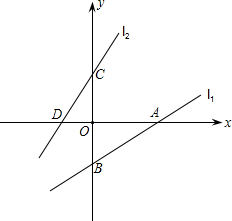 点A、B的坐标分别为A(2,0),B(0,1),解答下列问题:
点A、B的坐标分别为A(2,0),B(0,1),解答下列问题:(1)求点的坐标:C
(2)直线l1的解析式为
(3)直线l2的解析式为
(4)直线l1,l2交于点M,则点M的坐标为
(5)△ADM≌△
(6)△ADM的面积为
分析:(1)由A、B的坐标可以求出OA、OB,利用三角形全等可以求出OD=OB,OC=OA,从而求出点D、C的坐标.
(2)知道A、B两点的坐标直接用待定系数法就可以求出其解析式.
(3)利用C、D两点的坐标直接可以求出其解析式.
(4)利用两个函数的解析式建立二元一次方程组,方程组的解就是交点M的坐标.
(5)利用AAS可以证明△ADM≌△CBM
(6)求出AD的长,知道M的坐标的纵坐标就是△ADM的边AD上的高.就可以求出其面积.
(2)知道A、B两点的坐标直接用待定系数法就可以求出其解析式.
(3)利用C、D两点的坐标直接可以求出其解析式.
(4)利用两个函数的解析式建立二元一次方程组,方程组的解就是交点M的坐标.
(5)利用AAS可以证明△ADM≌△CBM
(6)求出AD的长,知道M的坐标的纵坐标就是△ADM的边AD上的高.就可以求出其面积.
解答: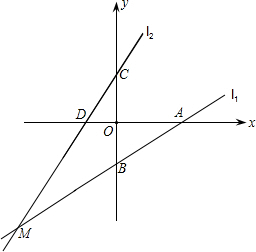 解:(1)∵△AOB≌△COD
解:(1)∵△AOB≌△COD
∴AO=CO,BO=DO,∠DCO=∠BAO
∵A(2,0),B(0,-1)
∴AO=2,BO=1
∴CO=2,DO=1
∴C(0,2),D(-1,0)
故答案为:C(0,2),D(-1,0)
(2)设l1的解析式为:y1=kx+b,由题意得
解得:
∴l1的解析式为:y1=
x-1
故答案为:y1=
x-1
(3)设l2的解析式为:y2=kx+b,由题意得
解得:
∴l2的解析式为:y2=2x+2
故答案为:y2=2x+2
(4)由题意得:
解得:
∴M(-2,-2)
故答案为:M(-2,-2)
(5)∵AO=CO,BO=DO
∴AO+DO=CO+BO
即AD=CB
∵∠DCO=∠BAO,∠DMB=∠DMB
∴△ADM≌△CBM
故答案为:△CBM
(6)∵A(2,0),D(-1,0)
∴AD=3,∵M(-2,-2)
∴AD边上的高为2,
∴S△ADM=
×2×3=3.
故答案为:3.
 解:(1)∵△AOB≌△COD
解:(1)∵△AOB≌△COD∴AO=CO,BO=DO,∠DCO=∠BAO
∵A(2,0),B(0,-1)
∴AO=2,BO=1
∴CO=2,DO=1
∴C(0,2),D(-1,0)
故答案为:C(0,2),D(-1,0)
(2)设l1的解析式为:y1=kx+b,由题意得
|
|
∴l1的解析式为:y1=
| 1 |
| 2 |
故答案为:y1=
| 1 |
| 2 |
(3)设l2的解析式为:y2=kx+b,由题意得
|
|
∴l2的解析式为:y2=2x+2
故答案为:y2=2x+2
(4)由题意得:
|
|
∴M(-2,-2)
故答案为:M(-2,-2)
(5)∵AO=CO,BO=DO
∴AO+DO=CO+BO
即AD=CB
∵∠DCO=∠BAO,∠DMB=∠DMB
∴△ADM≌△CBM
故答案为:△CBM
(6)∵A(2,0),D(-1,0)
∴AD=3,∵M(-2,-2)
∴AD边上的高为2,
∴S△ADM=
| 1 |
| 2 |
故答案为:3.
点评:本题是一道一次函数的综合试题,考查了三角形全等的性质与判定,三角形的面积,直线的交点坐标等多个知识点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
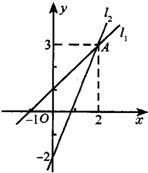 -2),结合图象解答下列问题:
-2),结合图象解答下列问题: 4、如图,直线l1,l2,l3相交于一点,则下列答案中,全对的一组是( )
4、如图,直线l1,l2,l3相交于一点,则下列答案中,全对的一组是( ) 如图,直线l1与l2相交于点O,OM⊥l1,若∠α=44°,则∠β等于
如图,直线l1与l2相交于点O,OM⊥l1,若∠α=44°,则∠β等于 如图,直线l1、l2、l3分别过正方形ABCD的三个顶点A,B,D,且相互平行,若l1与l2的距离为1,l2与l3的距离为1,则该正方形的面积是
如图,直线l1、l2、l3分别过正方形ABCD的三个顶点A,B,D,且相互平行,若l1与l2的距离为1,l2与l3的距离为1,则该正方形的面积是 如图,直线l1与l2相交于点P,l1的函数表达式y=kx+b,且经过(1,7)和(-3,-1)两点,点P的横坐标为-1,且l2交y轴于点A(0,-1).
如图,直线l1与l2相交于点P,l1的函数表达式y=kx+b,且经过(1,7)和(-3,-1)两点,点P的横坐标为-1,且l2交y轴于点A(0,-1).