题目内容
如图，直线l1、l2、l3分别过正方形ABCD的三个顶点A，B，D，且相互平行，若l1与l2的距离为1，l2与l3的距离为1，则该正方形的面积是5
5
．分析：首先过点B作BE⊥l1于E，过点D作DF⊥l1于F，由已知易证得△ADF≌△BAE，根据全等三角形的对应边相等，即可求得AE的长，然后由勾股定理，求得AB2的值，即可得该正方形的面积．
解答：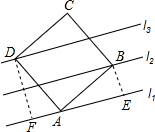
解：过点B作BE⊥l1于E，过点D作DF⊥l1于F，
∵l1与l2的距离为1，l2与l3的距离为1，l1∥l2∥l3，
∴DF=2，BE=1，∠DFA=∠AEB=90°，
∴∠ADF+∠DAF=90°，
∵四边形ABCD是正方形，
∴AD=AB，∠DAB=90°，
∴∠DAF+∠BAE=90°，
∴∠ADF=∠BAE，
在△ADF和△BAE中，
，
∴△ADF≌△BAE（AAS）
∴AE=DF=2，
在Rt△ABE中，AB2=AE2+BE2=12+22=5，
∴S正方形ABCD=5．
故答案为：5．
解：过点B作BE⊥l1于E，过点D作DF⊥l1于F，∵l1与l2的距离为1，l2与l3的距离为1，l1∥l2∥l3，
∴DF=2，BE=1，∠DFA=∠AEB=90°，
∴∠ADF+∠DAF=90°，
∵四边形ABCD是正方形，
∴AD=AB，∠DAB=90°，
∴∠DAF+∠BAE=90°，
∴∠ADF=∠BAE，
在△ADF和△BAE中，
|
∴△ADF≌△BAE（AAS）
∴AE=DF=2，
在Rt△ABE中，AB2=AE2+BE2=12+22=5，
∴S正方形ABCD=5．
故答案为：5．
点评：此题考查了正方形的性质、平行线间的距离、全等三角形的判定与性质以及勾股定理．此题难度适中，注意掌握辅助线的作法，注意数形结合思想的应用．
练习册系列答案
相关题目
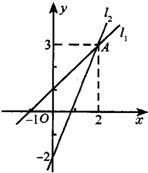-2），结合图象解答下列问题：
4、如图，直线l1，l2，l3相交于一点，则下列答案中，全对的一组是（ ）
如图，直线l1与l2相交于点O，OM⊥l1，若∠α=44°，则∠β等于
如图，直线l1与l2相交于点P，l1的函数表达式y=kx+b，且经过（1，7）和（-3，-1）两点，点P的横坐标为-1，且l2交y轴于点A（0，-1）．