题目内容
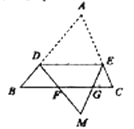
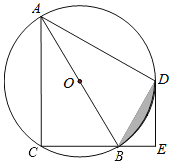
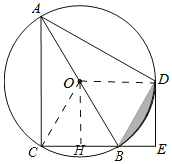
【题目】如图,四边形ACBD是⊙O的内接四边形,AB为直径,弧CD=弧AD,DE⊥BC,垂足为E.
(1)求证:BD平分∠ABE;
(2)判断直线ED与⊙O的位置关系,并说明理由;
(3)若BE=2,AB=8,求阴影部分的面积.
【答案】(1)见解析;(2)直线DE与圆O相切,理由见解析;(3)阴影部分的面积=![]() π-
π-![]() .
.
【解析】
(1)根据圆周角定理,由弧CD=弧AD,得到∠CAD=∠ABD,再根据圆内接四边形的性质得∠DBE=∠CAD,所以∠ABD=∠DBE;
(2)连结OD,如图,利用内错角相等证明OD∥CE,而DE⊥BC,则OD⊥DE,于是根据切线的判定定理可得DE为⊙O的切线;
(3)利用扇形面积公式、等边三角形的面积公式和阴影部分的面积解答即可.
证明:(1)∵弧CD=弧AD,
∴∠CAD=∠ABD,
∵∠DBE=∠CAD,
∴∠ABD=∠DBE.
即BD平分∠ABE
(2)直线DE与圆O相切,理由如下:
连结OD,OC,如图,
∵OB=OD,
∴∠OBD=∠ODB,
而∠OBD=∠DBE,
∴∠ODB=∠DBE,
∴OD∥CE,
∵DE⊥BC,
∴OD⊥DE,
∴DE为⊙O的切线
(3)作OH⊥BC于H,则四边形ODEH为矩形,
∴OD=EH,
∵BE=2,AB=8,
∴OB=OD=BD=4,
∴在Rt△DBE中,∠BDE=30°,
∴DE=2![]() ,
,
∴阴影部分的面积=![]() π-
π-![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目