题目内容
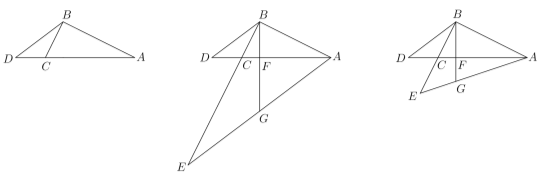
【题目】如图,已知△ABC,以AC为底边作等腰△ACD,且使∠ABC=2∠CAD,连接BD.

(1)如图1,若∠ADC=90°,∠BAC=30°,BC=1,求CD的长;
(2)如图1,若∠ADC=90°,证明:AB+BC=![]() BD;
BD;
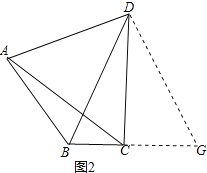
(3)如图2,若∠ADC=60°,探究AB,BC,BD之间的数量关系并证明.
【答案】见解析
【解析】
试题分析:(1)根据等腰直角三角形的性质和已知求出CD的长;
(2)作DE⊥AB于E,DF⊥BC交BC的延长线于F,证明△AED≌△CFD,得到DE=DF,AE=CF,根据正方形的性质证明结论;
(3)延长BC至G,使CG=AB,证明△DAB≌△DCG,得到△DBG是等边三角形,得到答案.
解:(1)∵∠ADC=90°,DA=DC,
∴∠CAD=45°,
∴∠ABC=2∠CAD=90°,又∠BAC=30°,
∴AC=2BC=2,
∴CD=AC×sin∠CAD=![]() ;
;
(2)作DE⊥AB于E,DF⊥BC交BC的延长线于F,
∵∠ADC=90°,DA=DC,
∴∠CAD=45°,
∴∠ABC=2∠CAD=90°,
∴四边形DEBF是矩形,
∵∠ABC=∠ADC=90°,
∴∠BAD+∠BCD=180°,
∴∠BAD=∠FCD,
在△AED和△CFD中,
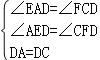 ,
,
∴△AED≌△CFD,
∴DE=DF,AE=CF,
∵四边形DEBF是矩形,DE=DF,
∴四边形DEBF是正方形,
∴BE=BF=![]() BD,又AE=CF,
BD,又AE=CF,
∴AB+BC=BE+BF=![]() BD;
BD;
(3)BD=AB+BC.
延长BC至G,使CG=AB,
∵∠ADC=60°和等腰△ACD,
∴△ACD是等边三角形,
∴∠ABC=2∠CAD=120°,
∴∠BAD+∠BCD=180°,
∴∠BAD=∠GCD,
在△DAB和△DCG中,
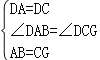 ,
,
∴△DAB≌△DCG,
∴DB=DG,∠CDG=∠ADB,又∠ADB+∠BDC=60°,
∠CDG+∠BDC=60°,
∴△DBG是等边三角形,
∴BD=BG=AB+BC.