��Ŀ����
����Ŀ���ۺ���ʵ�� ����Ļƽ����
�Ķ�����
����ѧ�ϳƶ̱��볤�ߵı���![]() ��ԼΪ0.618���ľ��ν����ƽ���Σ�GoldenRectangle�����ƽ�����̲��ŷḻ����ѧ��ֵ����������Э�����ȳƵ����У�
��ԼΪ0.618���ľ��ν����ƽ���Σ�GoldenRectangle�����ƽ�����̲��ŷḻ����ѧ��ֵ����������Э�����ȳƵ����У�
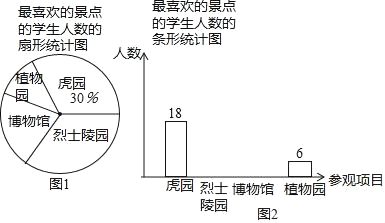
��1��ijУ��ί�ٰ��������ֳ������������ֳ������ͳһ��Ƴɣ�����40cm�Ļƽ���Σ����ԼΪ__________cm������ȷ��0.1cm��
�������� ����һ��������ֽƬ�۵���һ���ƽ���Σ�
��һ������ͼ1���۵�������ֽƬABCD��ʹAB��DC�غϣ��õ��ۺ�EF����E��F�ֱ��ڱ�AD��BC�ϣ���Ȼ���ֽƬչƽ��
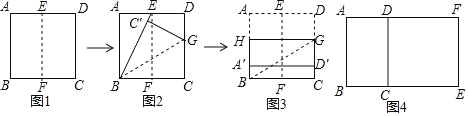
�ڶ�������ͼ2���۵�������ֽƬABCD��ʹ��BC����BE�ϣ���C���͵�C��Ӧ���õ��ۺ�BG����G��CD�ϣ����ٴ�ֽƬչƽ��
����������ͼ3���ع���G��ֱ���۵�������ֽƬABCD��ʹ��A�͵�D�ֱ�����AB��CD�ϣ��ۺ�ΪHG����Ȼ�ı���HBCGΪ���Σ�
��2�������������У���AB=2Ϊ����֤������HBCG�ǻƽ���Σ�
���ο����㣺![]() =
=![]() ��
��
�ع�̽��
��3����ϣ��С������ͬѧͨ��̽�����֣��Իƽ���εij���Ϊһ�ߣ���ԭ�ƽ�������������Σ��õ����¾�����Ȼ�ǻƽ���Σ�
��ͼ4������ı���ABCD�ǻƽ���Σ�AB��AD�����ı���DCEF�������Σ���ô�ı���ABEFҲ�ǻƽ���Σ����ǵķ�����ȷ����˵�����ɣ�
���𰸡���1��24.7����2��֤������������3���ı���ABEF�ǻƽ�������������ȷ.
��������
��1�����ݻƽ���εĶ�����㼴�ɣ�
��2����ͼ2�У�����EG����CG=C��G=x��������![]() ��Rt��EGD��Rt��EGC���У�
��Rt��EGD��Rt��EGC���� ![]() ���
���![]() �ɵ�
�ɵ�![]() ���ɴ˼���֤����
���ɴ˼���֤����
��3����ͼ4�У��ı���ABEF�ǻƽ�������������ȷ����AB=a����AD=BC=![]() a�����AB��BE��ֵ�����жϣ�
a�����AB��BE��ֵ�����жϣ�
�⣺��1����ԼΪ40��![]() ��40��0.681��24.7cm��
��40��0.681��24.7cm��
�ʴ�Ϊ24.7��
��2����ͼ2�У�����EG����CG=C��G=x��
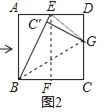
��AB=2��AE=ED=1��
��![]()
��Rt��EGD��Rt��EGC����![]()
���![]()
��![]()
��ͼ3�еľ���HBCG�ǻƽ���Σ�
��3����ͼ4�У��ı���ABEF�ǻƽ�������������ȷ��

���ɣ���AB=a����AD=BC=![]() a��
a��
���ı���DCEF�������Σ�
��DC=DF=EF=CE=a��
��![]()
��![]()
�����ABEF�ǻƽ���Σ�

 ��ڽ��ȫ������ϵ�д�
��ڽ��ȫ������ϵ�д�����Ŀ������������ӳ���ѵ������Ҫ��Ŀ֮һ������ͼ���е������Ǽס��ҡ�������ÿ��ʮ�ε�����Եijɼ������Թ���Ϊ��������10����ÿ����λ1����1�֣�
���������������������˶�Ա�ײ��Գɼ���
������� | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
�ɼ����֣� | 7 | 6 | 8 | 7 | 7 | 5 | 8 | 7 | 8 | 7 |
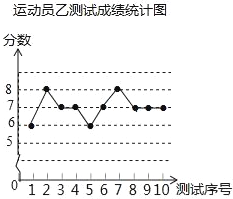
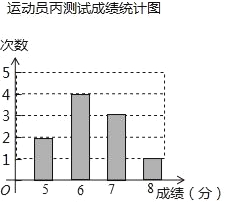
��1��д���˶�Ա�ײ��Գɼ�������Ϊ_____���˶�Ա�Ҳ��Գɼ�����λ��Ϊ_____���˶�Ա�����Գɼ���ƽ����Ϊ_____��
��2�����������˳ɼ��ķ���ֱ�ΪS��2=0.8��S��2=0.4��S��2=0.8�����ۺϷ�����������������ѡ��һλ����ɼ������ҽ�Ϊ�ȶ��Ľ���������Ϊ�����ˣ�����Ϊѡ˭�����ʣ�Ϊʲô��
��3���ס��ҡ��������֮����е�����ϰ��ÿ���˵��ȿ��ܵĴ����������ˣ������ȴӼ����д����������ֽ���ʱ��ص������еĸ����Ƕ��٣�������״ͼ���б������