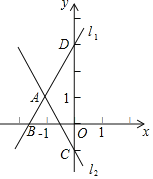题目内容
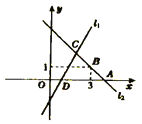
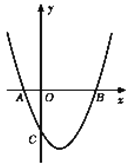
【题目】如图,抛物线![]() 与x轴交于A、B两点,与y轴交于点C(0,
与x轴交于A、B两点,与y轴交于点C(0,![]() ).
).
(1)![]() _____,点A的坐标为______,点B的坐标为_____;
_____,点A的坐标为______,点B的坐标为_____;
(2)设抛物线![]() 的顶点为M,求四边形ABMC的面积;
的顶点为M,求四边形ABMC的面积;
【答案】(1)-3(-1,0),(3,0)(2)9
【解析】
(1)把点C的坐标代入函数解析式,然后求出k的值即可;令y=0,得到关于x的一元二次方程,解方程求出x的值,再根据点A在点B的左边,写出坐标即可;
(2)把抛物线解析式整理成顶点式,然后写出顶点坐标,再连接OM,分别求出△AOC、△MOC、△MOB的面积,然后根据四边形ABMC的面积=△AOC的面积+△MOC的面积+△MOB的面积进行计算即可求解;
(1)∵抛物线y=x22x+k与y轴交于点C(0,3),
∴k=3,
∴抛物线的解析式为y=x22x3,
令y=0,则x22x3=0,
∴(x+1)(x3)=0,
∴x+1=0,x3=0,
解得x1=1,x2=3,
∴点A的坐标为A(1,0),点B的坐标为B(3,0);
故答案为:3,(1,0),(3,0);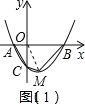
(2)如图(1),∵y=![]() 2x3=
2x3=![]() 4,
4,
∴抛物线的顶点为M(1,4),连接OM,
则△AOC的面积=![]() AOOC=
AOOC=![]() ×1×3=32,△MOC的面积=
×1×3=32,△MOC的面积=![]() OC|xM|=
OC|xM|=![]() ×3×1=
×3×1=![]() ,
,
△MOB的面积=![]() OB|yM|=
OB|yM|=![]() ×3×4=6,
×3×4=6,
∴四边形ABMC的面积=△AOC的面积+△MOC的面积+△MOB的面积=![]() +
+![]() +6=9.
+6=9.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目