题目内容
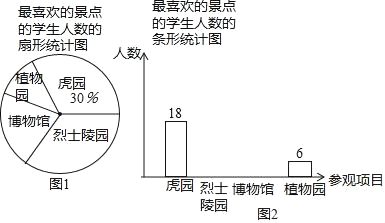
【题目】某校在一次社会实践活动中,组织学生参观了虎园、烈士陵园、博物馆和植物园,为了解本次社会实践活动的效果,学校随机抽取了部分学生,对“最喜欢的景点”进行了问卷调查,并根据统计结果绘制了如下不完整的统计图.其中最喜欢烈士陵园的学生人数与最喜欢博物馆的学生人数之比为2:1,请结合统计图解答下列问题:
(1)本次活动抽查了 名学生;
(2)请补全条形统计图;
(3)在扇形统计图中,最喜欢植物园的学生人数所对应扇形的圆心角是 度;
(4)该校此次参加社会实践活动的学生有720人,请求出最喜欢烈士陵园的人数约有多少人?
【答案】(1)60;(2)详见解析;(3)36;(4)288.
【解析】
(1)由虎园人数及其所占百分比可得总人数;
(2)设最喜欢博物馆的学生人数为x,则最喜欢烈士陵园的学生人数为2x,根据各参观项目人数和等于总人数求得x的值,据此即可补全图形;
(3)用360°乘以最喜欢植物园的学生人数占被调查人数的比例可得;
(4)用总人数乘以样本中最喜欢烈士陵园的人数所占比例.
(1)本次活动调查的学生人数为18÷30%=60人,
故答案为:60;
(2)设最喜欢博物馆的学生人数为x,则最喜欢烈士陵园的学生人数为2x,
则x+2x=60﹣18﹣6,
解得:x=12,
即最喜欢博物馆的学生人数为12,则最喜欢烈士陵园的学生人数为24,
补全条形图如下:
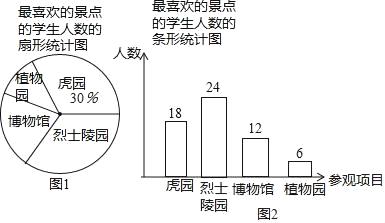
(3)在扇形统计图中,最喜欢植物园的学生人数所对应扇形的圆心角是360°×![]() =36°,
=36°,
故答案为:36;
(4)最喜欢烈士陵园的人数约有720×![]() =288人.
=288人.

练习册系列答案
相关题目