题目内容
下列命题错误的是
- A.经过不在同一直线上的三个点一定可以作圆
- B.三角形的外心到三角形各顶点的距离相等
- C.平分弦的直径垂直于弦,并且平分弦所对的两条弧
- D.经过切点且垂直于切线的直线必经过圆心
C
分析:根据确定圆的条件、三角形外心的性质、垂径定理的推论以及切线的性质分别进行判断即可.
解答:A、经过不共线的三点确定一个圆,所以A选项的命题正确;
B、三角形的外心是三条边的中垂线的交点,它到三角形三个顶点的距离相等,所以B选项的命题正确;
C、平分弦(非直径)的直径垂直于弦,并且平分弦所对的两条弧,所以C选项的命题错误;
D、经过切点且垂直于切线的直线必经过圆心,所以D选项的命题正确.
故选C.
点评:本题考查了垂径定理的推论:平分弦(非直径)的直径垂直于弦,并且平分弦所对的两条弧.也考查了确定圆的条件、三角形外心的性质以及切线的性质.
分析:根据确定圆的条件、三角形外心的性质、垂径定理的推论以及切线的性质分别进行判断即可.
解答:A、经过不共线的三点确定一个圆,所以A选项的命题正确;
B、三角形的外心是三条边的中垂线的交点,它到三角形三个顶点的距离相等,所以B选项的命题正确;
C、平分弦(非直径)的直径垂直于弦,并且平分弦所对的两条弧,所以C选项的命题错误;
D、经过切点且垂直于切线的直线必经过圆心,所以D选项的命题正确.
故选C.
点评:本题考查了垂径定理的推论:平分弦(非直径)的直径垂直于弦,并且平分弦所对的两条弧.也考查了确定圆的条件、三角形外心的性质以及切线的性质.

练习册系列答案
相关题目
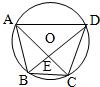 9、如图,已知四边形ABCD是⊙O的内接四边形,且AB=CD=5,AC=7,BE=3,下列命题错误的是( )
9、如图,已知四边形ABCD是⊙O的内接四边形,且AB=CD=5,AC=7,BE=3,下列命题错误的是( )