题目内容
 如图⊙O的直径为10,弦AB的长为8,如果点P是弦AB上的一个动点,那么线段OP的长度取值范围是多少?
如图⊙O的直径为10,弦AB的长为8,如果点P是弦AB上的一个动点,那么线段OP的长度取值范围是多少?
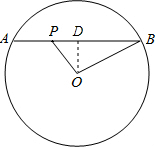 解:∵⊙O的直径为10,
解:∵⊙O的直径为10,∴OP最长时为5;
过点O作OD⊥AB于点D,
∵AB=8,
∴BD=4,
∴OD=
 =
= =3,
=3,∴OP最短时等于3,
∴3≤OP≤5.
分析:由于OP最长应是半径长,根据垂线段最短,可得到当OP⊥AB时,OP最短.再过点O作OD⊥AB于点D,根据垂径定理和勾股定理求解即可.
点评:本题考查的是垂径定理及勾股定理,解答此题的关键是熟知OP最长应是半径长,当OP⊥AB时,OP最短.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
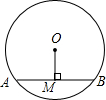 已知如图⊙O的直径为10,圆心O到弦AB的距离OM的长为3,则弦AB的长是( )
已知如图⊙O的直径为10,圆心O到弦AB的距离OM的长为3,则弦AB的长是( )| A、4 | B、6 | C、7 | D、8 |
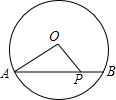 如图⊙O的直径为10,弦AB=8,P是弦AB上的一个动点,那么OP长的取值范围是( )
如图⊙O的直径为10,弦AB=8,P是弦AB上的一个动点,那么OP长的取值范围是( )| A、3≤OP≤5 | B、4≤OP≤5 | C、4≤OP≤8 | D、8≤OP≤10 |
 如图⊙O的直径为10,弦AB的长为8,如果点P是弦AB上的一个动点,那么线段OP的长度取值范围是多少?
如图⊙O的直径为10,弦AB的长为8,如果点P是弦AB上的一个动点,那么线段OP的长度取值范围是多少?
