ћвƒњƒЏ»Ё
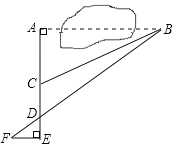
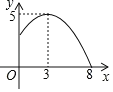
°Њћвƒњ°њƒ≥–°«ш”–“ї∞лЊґќ™8mµƒ‘≤–ќ≈зЋЃ≥Ў£ђ≈зЋЃ≥Ўµƒ÷№±я”–“ї»¶≈зЋЃЌЈ£ђ≈з≥цµƒЋЃ÷щќ™≈„ќпѕя£Ѓ‘ЏЊаЋЃ≥Ў÷––ƒ3mі¶іпµљ„оЄя£ђЄяґ»ќ™5m£ђ«“ЄчЄцЈљѕт≈з≥цµƒЋЃ÷щ«°Ї√‘Џ≈зЋЃ≥Ў÷––ƒµƒ„∞ ќќпі¶їгЇѕ£Ѓ“‘ЋЃ∆љЈљѕтќ™x÷б£ђ≈зЋЃ≥Ў÷––ƒќ™‘≠µгљ®ЅҐ»зЌЉЋщ Њµƒ∆љ√ж÷±љ«„ш±кѕµ£Ѓ
£®1£©«уЋЃ÷щЋщ‘Џ≈„ќпѕяґ‘”¶µƒЇѓ эєЎѕµ љ£ї
£®2£©Ќх ¶Єµ‘Џ≈зЋЃ≥Ўќђ–ё…и±Є∆ЏЉд£ђ≈зЋЃє№“вЌв≈зЋЃ£ђќ™ЅЋ≤ї±їЅ№ ™£ђ…нЄя1.8mµƒЌх ¶Єµ’ЊЅҐ ±±Ў–л‘ЏјлЋЃ≥Ў÷––ƒґа…ў√„“‘ƒЏ£њ
°Њір∞Є°њ£®1£©![]() £ї£®2£©7√„£Ѓ
£ї£®2£©7√„£Ѓ
°Њљвќц°њ
£®1£©ЄщЊЁґ•µг„ш±књ……иґюіќЇѓ эµƒґ•µг љ£ђіъ»лµг£®8£ђ0£©£ђ«у≥цa÷µ£ђіЋћвµ√љв£ї
£®2£©јы”√ґюіќЇѓ эЌЉѕу…ѕµгµƒ„ш±кћЎ’ч£ђ«у≥цµ±y=1.8 ±xµƒ÷µ£ђ”…іЋЉіњ…µ√≥цљб¬џ£Ѓ
љв£Ї£®1£©…иЋЃ÷щЋщ‘Џ≈„ќпѕя£®µЏ“їѕуѕё≤њЈ÷£©µƒЇѓ э±ніп љќ™y=a£®x©Б3£©2+5£®a°ў0£©£ђ
љЂ£®8£ђ0£©іъ»лy=a£®x©Б3£©2+5£ђµ√£Ї25a+5=0£ђ
љвµ√£Їa=©Б![]() £ђ
£ђ
°аЋЃ÷щЋщ‘Џ≈„ќпѕяµƒЇѓ э±ніп љќ™y=©Б![]() £®x©Б3£©2+5£®0£Љx£Љ8£©£Ѓ
£®x©Б3£©2+5£®0£Љx£Љ8£©£Ѓ
£®2£©µ±y=1.8 ±£ђ”–©Б![]() £®x©Б3£©2+5=1.8£ђ
£®x©Б3£©2+5=1.8£ђ
љвµ√£Їx1=©Б1£ђx2=7£ђ
°аќ™ЅЋ≤ї±їЅ№ ™£ђ…нЄя1.8√„µƒЌх ¶Єµ’ЊЅҐ ±±Ў–л‘ЏјлЋЃ≥Ў÷––ƒ7√„“‘ƒЏ£Ѓ