题目内容
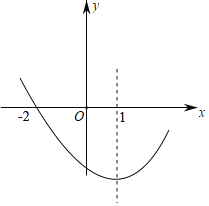
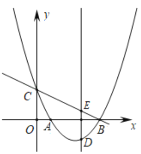
【题目】如图,抛物线![]() 与
与![]() 轴交于两点
轴交于两点![]() 和
和![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是抛物线上一个动点,过点
是抛物线上一个动点,过点![]() 作
作![]() 轴的垂线,与直线
轴的垂线,与直线![]() 相交于点
相交于点![]() .
.
(1)求抛物线的解析式;
(2)当点![]() 在直线
在直线![]() 下方的抛物线上运动时,线段
下方的抛物线上运动时,线段![]() 的长度是否存在最大值?存在的话,求出其最大值和此时点
的长度是否存在最大值?存在的话,求出其最大值和此时点![]() 的坐标;
的坐标;
(3)若以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形为平行四边形,求点
为顶点的四边形为平行四边形,求点![]() 的所有坐标.
的所有坐标.
【答案】(1)![]() ;(2)存在,DE取最大值2, D(2,﹣1);(3)点D的坐标是(2,﹣1)或
;(2)存在,DE取最大值2, D(2,﹣1);(3)点D的坐标是(2,﹣1)或![]() 或
或![]() .
.
【解析】
(1)利用待定系数法求解可得;
(2)设点D坐标为(m,![]() ),则E点的坐标为(m,
),则E点的坐标为(m,![]() ),求得DE关于m的函数关系式
),求得DE关于m的函数关系式![]() ,根据二次函数的性质即可求解;
,根据二次函数的性质即可求解;
(3)分点D在DE上方和下方两种情况,用![]() 的代数式表示出DE的长度,依据DE=2得出关于
的代数式表示出DE的长度,依据DE=2得出关于![]() 的方程,解之可得
的方程,解之可得
(1)把点A(1,0)、B(4,0)代入![]() ,得:
,得:
![]() ,
,
解得![]() ,
,
∴抛物线的解析式是![]() ;
;
(2)存在.
对于二次函数![]() ,
,
令![]() ,则
,则![]() ,
,
∴点C的坐标为(0,2),
设直线BC的解析式为y=kx+t,
把点B(4,0),C(0,2)代入y=kx+t,得:
![]() ,
,
解得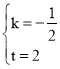 ,
,
∴![]() ;
;
设点D的坐标为![]() ,则点E的坐标为
,则点E的坐标为![]() ,
,
∴![]() ,
,
∴当m=2时,DE取最大值2,
此时![]() ,
,
∴点D的坐标为(2,﹣1);
(3)①当D在E下方时,
由(2)得:![]() ,
,
∵点C的坐标为(0,2),
∴OC=2,
∵OC∥DE,
∴当DE=OC时,四边形OCED为平行四边形,
则![]() ,
,
解得m=2,
此时点D的坐标为(2,﹣1);
②当D在E上方时,![]() ,
,
同理,当DE=OC时,四边形OCED为平行四边形,
即![]() ,
,
解得![]() ,
,
∴此时![]() 或
或![]() ,
,
综上所述,点D的坐标是(2,﹣1)或![]() 或
或![]() 时,都可以使O,C,D,E为顶点的四边形为平行四边形.
时,都可以使O,C,D,E为顶点的四边形为平行四边形.

 阅读快车系列答案
阅读快车系列答案【题目】为了发展学生的数学核心素养,培养学生的综合能力,某市开展了初三学生的数学 学业水平测试.在这次测试中,从甲、乙两校各随机抽取了 30 名学生的测试成绩进行调查分析
收集数据
甲校 | 94 | 82 | 77 | 76 | 77 | 88 | 90 | 88 | 85 | 86 | 88 | 89 | 84 | 92 | 87 |
88 | 80 | 53 | 89 | 91 | 91 | 86 | 68 | 75 | 94 | 84 | 76 | 69 | 83 | 92 | |
乙校 | 83 | 64 | 91 | 88 | 71 | 92 | 88 | 92 | 86 | 61 | 78 | 91 | 84 | 92 | 92 |
74 | 75 | 93 | 82 | 57 | 86 | 89 | 89 | 94 | 83 | 84 | 81 | 94 | 72 | 90 |
整理、描述数据 按如下分数段整理、描述这两组样本数据:
人数 成绩 x 学校 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
甲校 | 1 | 2 | 5 | 15 | 7 |
乙校 | 1 | 2 | 10 |
(说明:成绩 80 分及以上为优秀,60~79 分为合格,60 分以下为不合格) 分析数据 两组样本数据的平均数、中位数、众数如下表所示:
学校 | 平均数 | 中位数 | 众数 |
甲校 | 83.4 | 86 | 88 |
乙校 | 83.2 |
(1)请你补全表格;
(2)若甲校有 300 名学生,估计甲校此次测试的优秀人数为 ;
(3)可以推断出 校学生的成绩比较好,理由为 .