题目内容
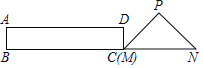
【题目】如图,在Rt△PMN中,∠P=90°,PM=PN,MN=6cm,矩形ABCD中AB=2cm,BC=10cm,点C和点M重合,点B、C(M)、N在同一直线上,令Rt△PMN不动,矩形ABCD沿MN所在直线以每秒1cm的速度向右移动,至点C与点N重合为止,设移动x秒后,矩形ABCD与△PMN重叠部分的面积为y,则y与x的大致图象是( )
A.  B.
B. 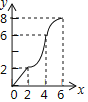 C.
C.  D.
D. 
【答案】A
【解析】在Rt△PMN中解题,要充分运用好垂直关系和45度角,因为此题也是点的移动问题,可知矩形ABCD以每秒1cm的速度由开始向右移动到停止,和Rt△PMN重叠部分的形状可分为下列三种情况,(1)0≤x≤2;(2)2<x≤4;(3)4<x≤6;根据重叠图形确定面积的求法,作出判断即可.
∵∠P=90°,PM=PN,
∴∠PMN=∠PNM=45°,
由题意得:CM=x,
分三种情况:
①当0≤x≤2时,如图1,
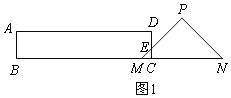
边CD与PM交于点E,
∵∠PMN=45°,
∴△MEC是等腰直角三角形,
此时矩形ABCD与△PMN重叠部分是△EMC,
∴y=S△EMC=![]() CMCE=
CMCE=![]() ;
;
故选项B和D不正确;
②如图2,
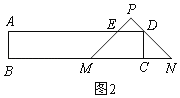
当D在边PN上时,过P作PF⊥MN于F,交AD于G,
∵∠N=45°,CD=2,
∴CN=CD=2,
∴CM=6﹣2=4,
即此时x=4,
当2<x≤4时,如图3,
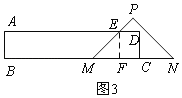
矩形ABCD与△PMN重叠部分是四边形EMCD,
过E作EF⊥MN于F,
∴EF=MF=2,
∴ED=CF=x﹣2,
∴y=S梯形EMCD=![]() CD(DE+CM)=
CD(DE+CM)=![]() =2x﹣2;
=2x﹣2;
③当4<x≤6时,如图4,
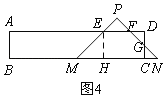
矩形ABCD与△PMN重叠部分是五边形EMCGF,过E作EH⊥MN于H,
∴EH=MH=2,DE=CH=x﹣2,
∵MN=6,CM=x,
∴CG=CN=6﹣x,
∴DF=DG=2﹣(6﹣x)=x﹣4,
∴y=S梯形EMCD﹣S△FDG=![]() ﹣
﹣![]() =
=![]() ×2×(x﹣2+x)﹣
×2×(x﹣2+x)﹣![]() =﹣
=﹣![]() +10x﹣18,
+10x﹣18,
故选项A正确;
故选:A.

 阅读快车系列答案
阅读快车系列答案