题目内容
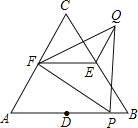
【题目】如图1,在平面直角坐标系xOy中,线段AB在x轴的正半轴上移动,且AB=1,过点A、B作y轴的平行线分别交函数y1=![]() (x>0)与y2=
(x>0)与y2=![]() (x>0)的图像于C、E和D、F,设点A的横坐标为m (m>0).
(x>0)的图像于C、E和D、F,设点A的横坐标为m (m>0).
(1)连接OC、OE,则△OCE面积为 ;
(2)连接CF,当m为何值时,四边形ABFC是矩形;
(3)连接CD、EF,判断四边形CDFE能否是平行四边形,并说明理由;
(4)如图2,经过点B和y轴上点G(0,4)作直线BG交直线AC于点H,若点H的纵坐标为正整数,请求出整数m的值.

【答案】(1)1;(2)![]() ;(3)不能;(4)m=1或3
;(3)不能;(4)m=1或3
【解析】
(1)先表示出点C,E坐标,再用三角形面积公式即可得出结论;
(2)先表示出点C,F坐标,利用矩形的性质对边相等建立方程求解即可得出结论;
(3)先表示出点C,D,E,F的坐标,进而求出CE,DF,判断出CE≠DF,即可得出结论;
(4)先求出直线BG的解析式,进而表示出点H的坐标,最后用![]() 是正整数,建立方程即可得出结论.
是正整数,建立方程即可得出结论.
(1)∵点A的横坐标为m,且AC∥y轴,
∴C(m,![]() ,E(m,
,E(m,![]() ),
),
∴S△COE=![]() CE×OA=
CE×OA=![]() (
(![]() ﹣
﹣![]() )m=1,
)m=1,
故答案为:1;
(2)若四边形ABFC是矩形,则 AC=BF,
∵AB=1,点A的横坐标为m,
∴点B的横坐标为:m+1
∴C(m,![]() ),F(m+1,
),F(m+1,![]() ),
),
∴AC=![]() ,FB=
,FB=![]() ,
,
∴![]() =
=![]() ,
,
∴m=![]() ;
;
(3)不能,
理由:由题意得,C(m,![]() ),E(m,
),E(m,![]() ),D(m+1,
),D(m+1,![]() ,F(m+1,
,F(m+1,![]() ),
),
∴CE=![]() ﹣
﹣![]() =
=![]() ,DF=
,DF=![]() ﹣
﹣![]() =
=![]() ,
,
∴CE≠DF,
∵CE∥DF,
∴四边形CDFE不是平行四边形;
(4)∵G(0,4),
∴设直线BG的表达式为y=kx+4(k≠0),
将B(m+1,0)代入y=kx+4中得k(m+1)+4=0,
∴k=﹣![]() ,
,
∴直线BG的解析式为y=﹣![]() x+4,
x+4,
将x=m代入y=﹣![]() x+4中得y=﹣
x+4中得y=﹣![]() x+4=
x+4=![]() ,
,
∴点H(m,![]() ),
),
∵m>0,
∴m+1>1,
∵点H的纵坐标是正整数,
∴m+1=2或m+1=4,
∴m=1或3.

 阅读快车系列答案
阅读快车系列答案