ΧβΡΩΡΎ»ί
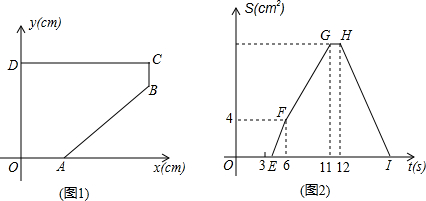
»γΆΦΔΌΘ§AΓΔDΖ÷±π‘Ύx÷αΚΆy÷α…œΘ§CDΓΈx÷αΘ§BCΓΈy÷αΘ°ΒψP¥”DΒψ≥ωΖΔΘ§“‘1cm/sΒΡΥΌΕ»Θ§―ΊΈε±Ώ–ΈOABCDΒΡ±Ώ‘»ΥΌ‘ΥΕ·“Μ÷ήΘ°Φ«Υ≥¥ΈΝΣΫαPΓΔOΓΔD»ΐΒψΥυΈß≥…ΆΦ–ΈΒΡΟφΜΐΈΣScm2Θ§ΒψP‘ΥΕ·ΒΡ ±ΦδΈΣt sΘ°“―÷ΣS”κt÷°ΦδΒΡΚ· ΐΙΊœΒ»γΆΦΔΎ÷–’έœΏΕΈOEFGHIΥυ ΨΘ°
‘ΡΕΝάμΫβΘ§≤ΔΜΊ¥πœ¬Ν–Έ ΧβΘΚ
Θ®1Θ©¥”ΆΦΔΎΒψEΩ…“‘Ω¥≥ωΗ’ΩΣ ΦΒΡ ±ΚρΘ§ΥφΉ≈ΒψPΒΡ‘ΥΕ·Θ§ΟφΜΐS≤ΔΟΜ”–ΖΔ…ζ±δΜ·Θ§”…¥ΥΩ…“‘≈–ΕœΒψPΒΡ‘ΥΕ·ΖΫœρΈΣ Θ®Χν»κΥ≥ ±’κΜρΡφ ±’κΘ©
Θ®2Θ©¥”ΆΦΔΎΒψFΘ®6Θ§4Θ©Ω…“‘ΒΟΒΫΘΚOD+OA=6ΘΜ
ODΓΝOA=4Θ§«“ODΘΨ3Θ°”…¥ΥΩ…“‘ΒΟΒΫODΓΔOAΒΡ≥ΛΕ»Θ§Ϋχ“Μ≤ΫΖ÷ΈωΘ§Ω…“‘«σΒΟAΓΔBΝΫΒψΒΡΉχ±ξΘΚAΘ® Θ§ Θ©ΓΔBΘ® Θ§ Θ©ΘΜ
Θ®3Θ©ΧΫΨΩ1ΘΚ «Ζώ¥φ‘ΎΡ≥“Μ ±ΩΧΘ§÷±œΏPDΫΪΈε±Ώ–ΈOABCDΖ÷≥…÷ή≥ΛœύΒ»ΒΡΝΫ≤ΩΖ÷ΘΩ»γΙϊ¥φ‘ΎΘ§Φρ“ΣΥΒΟς’β ±ΒψPΒΡΉχ±ξΘΜ»γΙϊ≤Μ¥φ‘ΎΘ§ΥΒΟςάμ”…Θ°
Θ®4Θ©ΧΫΨΩ2ΘΚ «Ζώ¥φ‘ΎΡ≥“Μ ±ΩΧΘ§÷±œΏPDΫΪΈε±Ώ–ΈOABCDΖ÷≥…ΟφΜΐœύΒ»ΒΡΝΫ≤ΩΖ÷ΘΩ»γΙϊ¥φ‘ΎΘ§«σ≥ω÷±œΏPDΒΡΚ· ΐΫβΈω ΫΘΜ»γΙϊ≤Μ¥φ‘ΎΘ§ΥΒΟςάμ”…Θ°

‘ΡΕΝάμΫβΘ§≤ΔΜΊ¥πœ¬Ν–Έ ΧβΘΚ
Θ®1Θ©¥”ΆΦΔΎΒψEΩ…“‘Ω¥≥ωΗ’ΩΣ ΦΒΡ ±ΚρΘ§ΥφΉ≈ΒψPΒΡ‘ΥΕ·Θ§ΟφΜΐS≤ΔΟΜ”–ΖΔ…ζ±δΜ·Θ§”…¥ΥΩ…“‘≈–ΕœΒψPΒΡ‘ΥΕ·ΖΫœρΈΣ
Θ®2Θ©¥”ΆΦΔΎΒψFΘ®6Θ§4Θ©Ω…“‘ΒΟΒΫΘΚOD+OA=6ΘΜ
| 1 |
| 2 |
Θ®3Θ©ΧΫΨΩ1ΘΚ «Ζώ¥φ‘ΎΡ≥“Μ ±ΩΧΘ§÷±œΏPDΫΪΈε±Ώ–ΈOABCDΖ÷≥…÷ή≥ΛœύΒ»ΒΡΝΫ≤ΩΖ÷ΘΩ»γΙϊ¥φ‘ΎΘ§Φρ“ΣΥΒΟς’β ±ΒψPΒΡΉχ±ξΘΜ»γΙϊ≤Μ¥φ‘ΎΘ§ΥΒΟςάμ”…Θ°
Θ®4Θ©ΧΫΨΩ2ΘΚ «Ζώ¥φ‘ΎΡ≥“Μ ±ΩΧΘ§÷±œΏPDΫΪΈε±Ώ–ΈOABCDΖ÷≥…ΟφΜΐœύΒ»ΒΡΝΫ≤ΩΖ÷ΘΩ»γΙϊ¥φ‘ΎΘ§«σ≥ω÷±œΏPDΒΡΚ· ΐΫβΈω ΫΘΜ»γΙϊ≤Μ¥φ‘ΎΘ§ΥΒΟςάμ”…Θ°
ΩΦΒψΘΚ“Μ¥ΈΚ· ΐΉέΚœΧβ
Ή®ΧβΘΚ
Ζ÷ΈωΘΚΘ®1Θ©ΗυΨί¥”ΆΦΔΎΒψEΩ…“‘Ω¥≥ωΗ’ΩΣ ΦΒΡ ±ΚρΘ§ΥφΉ≈ΒψPΒΡ‘ΥΕ·Θ§ΟφΜΐS≤ΔΟΜ”–ΖΔ…ζ±δΜ·Θ§Ι ΒψP‘ΎOD…œΘ§”…¥ΥΦ¥Ω…ΒΟ≥ωΫα¬έΘΜ
Θ®2Θ©œ»Ν§Ϋ”ADΘ§…ηΒψAΒΡΉχ±ξΈΣΘ®aΘ§0Θ©Θ§”…ΆΦ2ΒΟ≥ωDO=6-AOΚΆSΓςAOD=4Θ§Φ¥Ω…ΒΟ≥ω
DO•AO=4Θ§¥”ΕχΒΟ≥ωaΒΡ÷ΒΘ§‘ΌΗυΨίΆΦ2ΒΟ≥ωAΒΡΉχ±ξΘ§‘Ό―”≥ΛCBΫΜx÷α”ΎMΘ§ΗυΨίDΒψΒΡΉχ±ξΒΟ≥ωAB=5cmΘ§CB=1cmΘ§Φ¥Ω…«σ≥ωAM=
=4Θ§¥”ΕχΒΟ≥ωΒψBΒΡΉχ±ξΘΜ
Θ®3Θ©œ»ΗυΨίABCDΒΡΉχ±ξ«σ≥ωABΘ§BCΘ§CDΘ§ODΘ§OAΒΡ≥ΛΘ§ΫχΕχΩ…≈–Εœ≥ωPΒψΒΡΈΜ÷ΟΘ§ΙΐΒψPΉςPKΓΆx÷αΘ§ΗυΨίœύΥΤ»ΐΫ«–ΈΒΡ–‘÷ Ω…ΒΟ≥ωPKΒΡ≥ΛΘ§ΫχΕχΒΟ≥ωPΒψΉχ±ξΘΜ
Θ®4Θ©œ»…ηΒψPΘ®xΘ§yΘ©Θ§Ν§PCΓΔPOΘ§ΒΟ≥ωSΥΡ±Ώ–ΈDPBCΒΡΟφΜΐΘ§‘ΌΫχ––’ϊάμΘ§Φ¥Ω…ΒΟ≥ωx”κyΒΡΙΊœΒΘ§‘Ό”…AΘ§BΒψΒΡΉχ±ξΘ§«σ≥ω÷±œΏABΒΡΚ· ΐΙΊœΒ ΫΘ§¥”Εχ«σ≥ωxΓΔyΒΡ÷ΒΘ§Φ¥Ω…ΒΟ≥ωPΒψΒΡΉχ±ξΘ§‘Ό…η÷±œΏPDΒΡΚ· ΐΙΊœΒ ΫΈΣy=kx+4Θ§«σ≥ωKΒΡ÷ΒΘ§Φ¥Ω…ΒΟ≥ω÷±œΏPDΒΡΚ· ΐΙΊœΒ ΫΘ°
Θ®2Θ©œ»Ν§Ϋ”ADΘ§…ηΒψAΒΡΉχ±ξΈΣΘ®aΘ§0Θ©Θ§”…ΆΦ2ΒΟ≥ωDO=6-AOΚΆSΓςAOD=4Θ§Φ¥Ω…ΒΟ≥ω
| 1 |
| 2 |
| AB2-MB2 |
Θ®3Θ©œ»ΗυΨίABCDΒΡΉχ±ξ«σ≥ωABΘ§BCΘ§CDΘ§ODΘ§OAΒΡ≥ΛΘ§ΫχΕχΩ…≈–Εœ≥ωPΒψΒΡΈΜ÷ΟΘ§ΙΐΒψPΉςPKΓΆx÷αΘ§ΗυΨίœύΥΤ»ΐΫ«–ΈΒΡ–‘÷ Ω…ΒΟ≥ωPKΒΡ≥ΛΘ§ΫχΕχΒΟ≥ωPΒψΉχ±ξΘΜ
Θ®4Θ©œ»…ηΒψPΘ®xΘ§yΘ©Θ§Ν§PCΓΔPOΘ§ΒΟ≥ωSΥΡ±Ώ–ΈDPBCΒΡΟφΜΐΘ§‘ΌΫχ––’ϊάμΘ§Φ¥Ω…ΒΟ≥ωx”κyΒΡΙΊœΒΘ§‘Ό”…AΘ§BΒψΒΡΉχ±ξΘ§«σ≥ω÷±œΏABΒΡΚ· ΐΙΊœΒ ΫΘ§¥”Εχ«σ≥ωxΓΔyΒΡ÷ΒΘ§Φ¥Ω…ΒΟ≥ωPΒψΒΡΉχ±ξΘ§‘Ό…η÷±œΏPDΒΡΚ· ΐΙΊœΒ ΫΈΣy=kx+4Θ§«σ≥ωKΒΡ÷ΒΘ§Φ¥Ω…ΒΟ≥ω÷±œΏPDΒΡΚ· ΐΙΊœΒ ΫΘ°
Ϋβ¥πΘΚ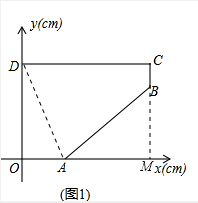 ΫβΘΚΘ®1Θ©ΓΏ¥”ΆΦΔΎΒψEΩ…“‘Ω¥≥ωΗ’ΩΣ ΦΒΡ ±ΚρΘ§ΥφΉ≈ΒψPΒΡ‘ΥΕ·Θ§ΟφΜΐS≤ΔΟΜ”–ΖΔ…ζ±δΜ·Θ§
ΫβΘΚΘ®1Θ©ΓΏ¥”ΆΦΔΎΒψEΩ…“‘Ω¥≥ωΗ’ΩΣ ΦΒΡ ±ΚρΘ§ΥφΉ≈ΒψPΒΡ‘ΥΕ·Θ§ΟφΜΐS≤ΔΟΜ”–ΖΔ…ζ±δΜ·Θ§
ΓύΒψP‘ΎOD…œΘ§
ΓΏΒψP¥”DΒψ≥ωΖΔΘ§“‘1cm/sΒΡΥΌΕ»―ΊΈε±Ώ–ΈOABCDΒΡ±Ώ‘»ΥΌ‘ΥΕ·“Μ÷ήΘ§
ΓύΒψPΒΡ‘ΥΕ·ΖΫœρΈΣΡφ ±’κΘ°
Ι ¥πΑΗΈΣΘΚΡφ ±’κΘΜ
Θ®2Θ©Ν§Ϋ”ADΘ§…ηΒψAΒΡΉχ±ξΈΣΘ®aΘ§0Θ©Θ§
”…ΆΦ2÷ΣΘ§DO+OA=6cmΘ§‘ρDO=6-AO=6-aΘ§
”…ΆΦ2÷ΣSΓςAOD=4Θ§
Γύ
DO•AO=
aΘ®6-aΘ©=4Θ§
’ϊάμΒΟΘΚa2-6a+8=0Θ§
ΫβΒΟa=2Μρa=4Θ§
”…ΆΦ2÷ΣΘ§DOΘΨ3Θ§
ΓύAOΘΦ3Θ§
Γύa=2Θ§
ΓύAΒΡΉχ±ξΈΣΘ®2Θ§0Θ©Θ§
DΒψΉχ±ξΈΣΘ®0Θ§4Θ©Θ§
‘ΎΆΦ1÷–Θ§―”≥ΛCBΫΜx÷α”ΎMΘ§
”…ΆΦ2Θ§÷ΣAB=5cmΘ§CB=1cmΘ§
ΓύMB=3Θ§
ΓύAM=
=4Θ°
ΓύOM=6Θ§
ΓύBΒψΉχ±ξΈΣΘ®6Θ§3Θ©Θ°
Ι ¥πΑΗΈΣΘΚΘ®2Θ§0 Θ©ΓΔΘ® 6Θ§3 Θ©ΘΜ

Θ®3Θ©¥φ‘ΎΘ°
άμ”…ΘΚΓΏ”…Θ®1Θ©÷ΣΘ§AΘ®2Θ§0Θ©Θ§BΘ®6Θ§3Θ©Θ§DΘ®0Θ§4Θ©Θ§
ΓύCΘ®6Θ§4Θ©Θ§
ΓύOA=2Θ§AB=5Θ§BC=1Θ§CD=6Θ§OD=4Θ§
ΓύΈε±Ώ–ΈOABCDΒΡ÷ή≥Λ=2+5+1+6+4=18Θ§
ΓΏ÷±œΏPDΫΪΈε±Ώ–ΈOABCDΖ÷≥…÷ή≥ΛœύΒ»ΒΡΝΫ≤ΩΖ÷Θ§
ΓύΒψP‘ΎœΏΕΈAB…œΘ§«“ΨύΒψB2ΗωΒΞΈΜ≥ΛΕ»Θ§
ΓύAP=3Θ§
Γύ
=
Θ§Φ¥
=
Θ§ΫβΒΟPK=
Θ§
ΓύAK=
=
=
Θ§
ΓΏOA=2Θ§
ΓύOK=2+
=
Θ§
ΓύPΘ®
Θ§
Θ©ΘΜ
Θ®4Θ©¥φ‘ΎΘ°
άμ”…ΘΚ»γΆΦ3Θ§ΓΏP‘ΎOAΓΔBCΓΔCD…œ ±Θ§÷±œΏPDΕΦ≤ΜΡήΫΪΈε±Ώ–ΈOABCDΖ÷≥…ΟφΜΐœύΒ»ΒΡΝΫ≤ΩΖ÷Θ§
Γύ÷Μ”–ΒψP“ΜΕ®‘ΎAB…œ ±Θ§≤≈ΡήΫΪΈε±Ώ–ΈOABCDΖ÷≥…ΟφΜΐœύΒ»ΒΡΝΫ≤ΩΖ÷Θ§
…ηΒψPΘ®xΘ§yΘ©Θ§Ν§PCΓΔPOΘ§‘ρ
SΥΡ±Ώ–ΈDPBC=SΓςDPC+SΓςPBC=
SΈε±Ώ–ΈOABCD=
Θ®SΨΊ–ΈOMCD-SΓςABMΘ©=9Θ§
Γύ
6ΓΝΘ®4-yΘ©+
ΓΝ1ΓΝΘ®6-xΘ©=9Θ§
Φ¥x+6y=12Θ§
Ά§άμΘ§”…SΥΡ±Ώ–ΈDPAO=9Ω…ΒΟ2x+y=9Θ§
”…
Θ§
ΫβΒΟx=
Θ§y=
Θ°
ΓύPΘ®
Θ§
Θ©Θ§
…η÷±œΏPDΒΡΚ· ΐΙΊœΒ ΫΈΣy=kx+4Θ®kΓΌ0Θ©Θ§
‘ρ
=
k+4Θ§
Γύk=-
Θ§
Γύ÷±œΏPDΒΡΚ· ΐΙΊœΒ ΫΈΣy=-
x+4Θ°
 ΫβΘΚΘ®1Θ©ΓΏ¥”ΆΦΔΎΒψEΩ…“‘Ω¥≥ωΗ’ΩΣ ΦΒΡ ±ΚρΘ§ΥφΉ≈ΒψPΒΡ‘ΥΕ·Θ§ΟφΜΐS≤ΔΟΜ”–ΖΔ…ζ±δΜ·Θ§
ΫβΘΚΘ®1Θ©ΓΏ¥”ΆΦΔΎΒψEΩ…“‘Ω¥≥ωΗ’ΩΣ ΦΒΡ ±ΚρΘ§ΥφΉ≈ΒψPΒΡ‘ΥΕ·Θ§ΟφΜΐS≤ΔΟΜ”–ΖΔ…ζ±δΜ·Θ§ΓύΒψP‘ΎOD…œΘ§
ΓΏΒψP¥”DΒψ≥ωΖΔΘ§“‘1cm/sΒΡΥΌΕ»―ΊΈε±Ώ–ΈOABCDΒΡ±Ώ‘»ΥΌ‘ΥΕ·“Μ÷ήΘ§
ΓύΒψPΒΡ‘ΥΕ·ΖΫœρΈΣΡφ ±’κΘ°
Ι ¥πΑΗΈΣΘΚΡφ ±’κΘΜ
Θ®2Θ©Ν§Ϋ”ADΘ§…ηΒψAΒΡΉχ±ξΈΣΘ®aΘ§0Θ©Θ§
”…ΆΦ2÷ΣΘ§DO+OA=6cmΘ§‘ρDO=6-AO=6-aΘ§
”…ΆΦ2÷ΣSΓςAOD=4Θ§
Γύ
| 1 |
| 2 |
| 1 |
| 2 |
’ϊάμΒΟΘΚa2-6a+8=0Θ§
ΫβΒΟa=2Μρa=4Θ§
”…ΆΦ2÷ΣΘ§DOΘΨ3Θ§
ΓύAOΘΦ3Θ§
Γύa=2Θ§
ΓύAΒΡΉχ±ξΈΣΘ®2Θ§0Θ©Θ§
DΒψΉχ±ξΈΣΘ®0Θ§4Θ©Θ§
‘ΎΆΦ1÷–Θ§―”≥ΛCBΫΜx÷α”ΎMΘ§
”…ΆΦ2Θ§÷ΣAB=5cmΘ§CB=1cmΘ§
ΓύMB=3Θ§
ΓύAM=
| AB2-MB2 |
ΓύOM=6Θ§
ΓύBΒψΉχ±ξΈΣΘ®6Θ§3Θ©Θ°
Ι ¥πΑΗΈΣΘΚΘ®2Θ§0 Θ©ΓΔΘ® 6Θ§3 Θ©ΘΜ

Θ®3Θ©¥φ‘ΎΘ°
άμ”…ΘΚΓΏ”…Θ®1Θ©÷ΣΘ§AΘ®2Θ§0Θ©Θ§BΘ®6Θ§3Θ©Θ§DΘ®0Θ§4Θ©Θ§
ΓύCΘ®6Θ§4Θ©Θ§
ΓύOA=2Θ§AB=5Θ§BC=1Θ§CD=6Θ§OD=4Θ§
ΓύΈε±Ώ–ΈOABCDΒΡ÷ή≥Λ=2+5+1+6+4=18Θ§
ΓΏ÷±œΏPDΫΪΈε±Ώ–ΈOABCDΖ÷≥…÷ή≥ΛœύΒ»ΒΡΝΫ≤ΩΖ÷Θ§
ΓύΒψP‘ΎœΏΕΈAB…œΘ§«“ΨύΒψB2ΗωΒΞΈΜ≥ΛΕ»Θ§
ΓύAP=3Θ§
Γύ
| AP |
| AB |
| PK |
| BM |
| 3 |
| 5 |
| PK |
| 3 |
| 9 |
| 5 |
ΓύAK=
| AP2-PK2 |
32-(
|
| 12 |
| 5 |
ΓΏOA=2Θ§
ΓύOK=2+
| 12 |
| 5 |
| 22 |
| 5 |
ΓύPΘ®
| 22 |
| 5 |
| 9 |
| 5 |
Θ®4Θ©¥φ‘ΎΘ°
άμ”…ΘΚ»γΆΦ3Θ§ΓΏP‘ΎOAΓΔBCΓΔCD…œ ±Θ§÷±œΏPDΕΦ≤ΜΡήΫΪΈε±Ώ–ΈOABCDΖ÷≥…ΟφΜΐœύΒ»ΒΡΝΫ≤ΩΖ÷Θ§
Γύ÷Μ”–ΒψP“ΜΕ®‘ΎAB…œ ±Θ§≤≈ΡήΫΪΈε±Ώ–ΈOABCDΖ÷≥…ΟφΜΐœύΒ»ΒΡΝΫ≤ΩΖ÷Θ§
…ηΒψPΘ®xΘ§yΘ©Θ§Ν§PCΓΔPOΘ§‘ρ
SΥΡ±Ώ–ΈDPBC=SΓςDPC+SΓςPBC=
| 1 |
| 2 |
| 1 |
| 2 |
Γύ
| 1 |
| 2 |
| 1 |
| 2 |
Φ¥x+6y=12Θ§

Ά§άμΘ§”…SΥΡ±Ώ–ΈDPAO=9Ω…ΒΟ2x+y=9Θ§
”…
|
ΫβΒΟx=
| 42 |
| 11 |
| 15 |
| 11 |
ΓύPΘ®
| 42 |
| 11 |
| 15 |
| 11 |
…η÷±œΏPDΒΡΚ· ΐΙΊœΒ ΫΈΣy=kx+4Θ®kΓΌ0Θ©Θ§
‘ρ
| 15 |
| 11 |
| 42 |
| 11 |
Γύk=-
| 29 |
| 42 |
Γύ÷±œΏPDΒΡΚ· ΐΙΊœΒ ΫΈΣy=-
| 29 |
| 42 |
ΒψΤάΘΚ±ΨΧβΩΦ≤ιΒΡ «“Μ¥ΈΚ· ΐΉέΚœΧβΘ§…φΦΑΒΫΕ·ΒψΈ ΧβΒΡΚ· ΐΆΦœσΘ§ΫβΧβΒΡΙΊΦϋ «ΗυΨίΧβ“β…η≥ωΚ· ΐΙΊœΒ ΫΘ§ «Ρ―ΒψΘ§“≤ «÷–ΩΦΒΡ÷ΊΒψΘ§–η λΝΖ’ΤΈ’Θ°

ΝΖœΑ≤αœΒΝ–¥πΑΗ
 νΦΌΉς“ΒΚΘ―ύ≥ωΑφ…γœΒΝ–¥πΑΗ
νΦΌΉς“ΒΚΘ―ύ≥ωΑφ…γœΒΝ–¥πΑΗ ±ΨΆΝΫΧΗ®”°‘Ύ νΦΌΗΏ–ßΦΌΤΎΉήΗ¥œΑ‘ΤΡœΩΤΦΦ≥ωΑφ…γœΒΝ–¥πΑΗ
±ΨΆΝΫΧΗ®”°‘Ύ νΦΌΗΏ–ßΦΌΤΎΉήΗ¥œΑ‘ΤΡœΩΤΦΦ≥ωΑφ…γœΒΝ–¥πΑΗ νΦΌΉς“Β±±Ψ©“’ θ”κΩΤ―ßΒγΉ”≥ωΑφ…γœΒΝ–¥πΑΗ
νΦΌΉς“Β±±Ψ©“’ θ”κΩΤ―ßΒγΉ”≥ωΑφ…γœΒΝ–¥πΑΗ ΒΎ»ΐ―ßΤΎ”°‘Ύ νΦΌœΒΝ–¥πΑΗ
ΒΎ»ΐ―ßΤΎ”°‘Ύ νΦΌœΒΝ–¥πΑΗ
œύΙΊΧβΡΩ
’ΐ»ΐΫ«–Έ–ΐΉΣ“ΜΕ®Ϋ«Ε»ΚσΡή”κΉ‘…μ÷ΊΚœΘ§‘ρ–ΐΉΣΒΡΫ«Ε»Ω…Ρή «Θ®ΓΓΓΓΘ©
| AΓΔ30Γψ | BΓΔ60Γψ |
| CΓΔ90Γψ | DΓΔ120Γψ |
Ιέ≤λΆΦ÷–ΒΡΆΦ–ΈΘ§ «÷––ΡΕ‘≥ΤΆΦ–ΈΒΡ”–Θ®ΓΓΓΓΘ© 

| AΓΔ2Ηω | BΓΔ1Ηω | CΓΔ4Ηω | DΓΔ3Ηω |
 »γΆΦΘ§Β»±Ώ»ΐΫ«–ΈABCΒΡ±Ώ≥ΛΈΣ1Θ§Ε·ΒψP¥”AΒψ≥ωΖΔΘ§―ΊΒ»±Ώ»ΐΫ«–ΈΒΡ±ΏΑ¥Ρφ ±’κΖΫœρ‘ΥΕ·Θ§Β±ΥϋΒΡ‘ΥΕ·ΒΡ¬Ζ≥ΧΈΣ2010 ±Θ§ΒψPΥυ‘ΎΒΡΈΜ÷ΟΈΣ
»γΆΦΘ§Β»±Ώ»ΐΫ«–ΈABCΒΡ±Ώ≥ΛΈΣ1Θ§Ε·ΒψP¥”AΒψ≥ωΖΔΘ§―ΊΒ»±Ώ»ΐΫ«–ΈΒΡ±ΏΑ¥Ρφ ±’κΖΫœρ‘ΥΕ·Θ§Β±ΥϋΒΡ‘ΥΕ·ΒΡ¬Ζ≥ΧΈΣ2010 ±Θ§ΒψPΥυ‘ΎΒΡΈΜ÷ΟΈΣ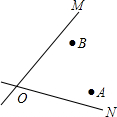 Βγ–≈≤ΩΟ≈“Σ–όΫ®“ΜΉυΒγ ”–≈Κ≈ΖΔ…δΥΰΘ§»γΆΦΥυ ΨΘ§Α¥’’…ηΦΤ“Σ«σΘ§ΖΔ…δΥΰΒΫΝΫΗω≥«’ρAΘ§BΒΡΨύάκœύΒ»Θ§ΒΫΝΫΧθΗΏΥΌΙΪ¬ΖOMΚΆONΒΡΨύάκ“≤±Ί–κœύΒ»Θ§ΖΔ…δΥΰ”ΠΫ®‘Ύ ≤Ο¥ΈΜ÷ΟΘΩ‘ΎΆΦ…œ±ξ≥ωΥϋΒΡΈΜ÷ΟΘ°
Βγ–≈≤ΩΟ≈“Σ–όΫ®“ΜΉυΒγ ”–≈Κ≈ΖΔ…δΥΰΘ§»γΆΦΥυ ΨΘ§Α¥’’…ηΦΤ“Σ«σΘ§ΖΔ…δΥΰΒΫΝΫΗω≥«’ρAΘ§BΒΡΨύάκœύΒ»Θ§ΒΫΝΫΧθΗΏΥΌΙΪ¬ΖOMΚΆONΒΡΨύάκ“≤±Ί–κœύΒ»Θ§ΖΔ…δΥΰ”ΠΫ®‘Ύ ≤Ο¥ΈΜ÷ΟΘΩ‘ΎΆΦ…œ±ξ≥ωΥϋΒΡΈΜ÷ΟΘ°