题目内容
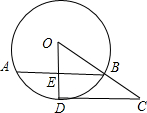如图，AB为⊙O的弦，过点O作OD⊥AB于点E，交⊙O于点D，过点D作CD∥AB，连接OB并延长交CD于点C，已知⊙O的半径为10，OE=6．求：（1）弦AB的长；（2）CD的长．
分析：（1）由于OD⊥AB，由勾股定理得OE2+BE2=OB2，BE=8；因为OE⊥AB，故AB=2BE=16；
（2）由于CD∥AB，易证△BOE∽△COD，根据三角形的相似比可求出CD的值．
（2）由于CD∥AB，易证△BOE∽△COD，根据三角形的相似比可求出CD的值．
解答：解：（1）∵OE2+BE2=OB2
∴BE=8．（2分）
又∵OE⊥AB，
∴AB=2BE=16．（4分）
（2）∵CD∥AB，
∴∠OBE=∠C．
又∠BOE=∠COD，
∴△BOE∽△COD． （6分）
∴
=
．
∴CD=
． （8分）
∴BE=8．（2分）
又∵OE⊥AB，
∴AB=2BE=16．（4分）
（2）∵CD∥AB，
∴∠OBE=∠C．
又∠BOE=∠COD，
∴△BOE∽△COD． （6分）
∴
| BE |
| CD |
| OE |
| OD |
∴CD=
| 40 |
| 3 |
点评：本题比较简单，考查的是相似三角形判定定理，勾股定理及垂径定理，是中学阶段的基本题目．
练习册系列答案
相关题目
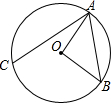如图，AB为⊙O的弦，∠AOB=100°，点C在⊙O上，且 
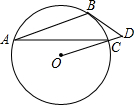已知：如图，AB为⊙O的弦，过点O作AB的平行线，交⊙O于点C，直线OC上一点D满足∠D=∠ACB．
54、如图，AB为⊙O的弦，C、D为直线AB上两点，要使OC=OD，则图中的线段必满足的条件是
（2012•闵行区三模）已知：如图，AB为⊙O的弦，OD⊥AB，垂足为点D，DO的延长线交⊙O于点C．过点C作CE⊥AO，分别与AB、AO的延长线相交于E、F两点．CD=8，sin∠A=
如图，AB为⊙0的弦，⊙0的半径为10，0C⊥AB于点D，交⊙0于点C，且CD=2，则弦AB的长是