题目内容
【题目】如图,□ABCD的对角线AC,BD交于点O,CE平分∠BCD交AB于点E,交BD于点F,且∠ABC=60°,AB=2BC,连接OE.下列结论:①EO⊥AC;②S△AOD=4S△OCF;③AC:BD=![]() :7;④FB2=OFDF.其中正确的是( )
:7;④FB2=OFDF.其中正确的是( )
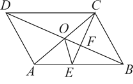
A.①②④B.①③④C.②③④D.①③
【答案】B
【解析】
①正确.只要证明EC=EA=BC,推出∠ACB=90°,再利用三角形中位线定理即可判断.
②错误.想办法证明BF=2OF,推出S△BOC=3S△OCF即可判断.
③正确.设BC=BE=EC=a,求出AC,BD即可判断.
④正确.求出BF,OF,DF(用a表示),通过计算证明即可.
解:∵四边形ABCD是平行四边形,
∴CD∥AB,OD=OB,OA=OC,
∴∠DCB+∠ABC=180°,
∵∠ABC=60°,
∴∠DCB=120°,
∵EC平分∠DCB,
∴∠ECB=![]() ∠DCB=60°,
∠DCB=60°,
∴∠EBC=∠BCE=∠CEB=60°,
∴△ECB是等边三角形,
∴EB=BC,
∵AB=2BC,
∴EA=EB=EC,
∴∠ACB=90°,
∵OA=OC,EA=EB,
∴OE∥BC,
∴∠AOE=∠ACB=90°,
∴EO⊥AC,故①正确,
∵OE∥BC,
∴△OEF∽△BCF,
∴![]() ,
,
∴OF=![]() OB,
OB,
∴S△AOD=S△BOC=3S△OCF,故②错误,
设BC=BE=EC=a,则AB=2a,AC=![]() a,OD=OB=
a,OD=OB=![]() a,
a,
∴BD=![]() a,
a,
∴AC:BD=![]() a:
a:![]() a=
a=![]() :7,故③正确,
:7,故③正确,
∵OF=![]() OB=
OB=![]() a,
a,
∴BF=![]() a,
a,
∴BF2=![]() a2,OFDF=
a2,OFDF=![]() a
a![]() a2,
a2,
∴BF2=OFDF,故④正确,
故选:B.

练习册系列答案
相关题目