Question

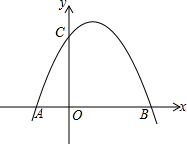（2013•道外区三模）如图，已知抛物线y=ax²+bx+c过点A（-1，0）、B（3，0）、C（0，3）
（1）求此抛物线的解析式．
（2）设抛物线的顶点为D，连接CD、BD，求△BCD的面积．

Answer 1

分析：（1）先把A、B、C三点的坐标代入解析式得到关于a、b、c的方程组，然后解方程组即可；
（2）先把抛物线解析式配成顶点式确定D点坐标，然后利用S_△BCD=S_{四边形OCDB}-S_△OBC=S_△BDH+S_梯形OCDH-S_△OBC进行计算．

解答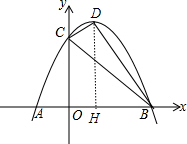：解：（1）根据题意得

a-b+c=0 9a+3b+c=0 c=3

，
解得

a=-1 b=2 c=3

，
所以抛物线的解析式为y=-x²+2x+3；

（2）如图，作DH⊥x轴于H，
∵y=-x²+2x+3=-（x-1）²+4，
∴顶点D的坐标为（1，4），
∴S_△BCD=S_{四边形OCDB}-S_△OBC
=S_△BDH+S_梯形OCDH-S_△OBC
=

1

2

×（3-1）×4+

1

2

×（3+4）×1-

1

2

×3×3=3．

点评：本题考查了用待定系数法求二次函数的解析式：在利用待定系数法求二次函数关系式时，要根据题目给定的条件，选择恰当的方法设出关系式，从而代入数值求解．一般地，当已知抛物线上三点时，常选择一般式，用待定系数法列三元一次方程组来求解；当已知抛物线的顶点或对称轴时，常设其解析式为顶点式来求解；当已知抛物线与x轴有两个交点时，可选择设其解析式为交点式来求解．