题目内容
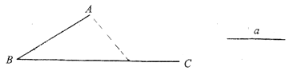
【题目】如图,在四边形ABCD中,CB=CD,∠D+∠ABC=180°,CE⊥AD于E.
(1)求证:AC平分∠DAB;
(2)若AE=3ED=6,求AB的长.
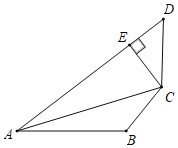
【答案】(1)证明见解析;(2)4.
【解析】
(1)过C点作CF⊥AB,交AB的延长线于点F.由AAS证明△CDE≌△CBF,可得CE=CF,结论得证;
(2)证明Rt△ACE≌Rt△ACF,可得AE=AF,可求出AB=4.
(1)证明:过C点作CF⊥AB,交AB的延长线于点F.
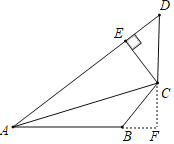
∵CE⊥AD,
∴∠DEC=∠CFB=90°,
∵∠D+∠ABC=180°,∠ABC+∠CBF=180°,
∴∠D=∠CBF,
∵CD=CB,
∴△CDE≌△CBF(AAS),
∴CE=CF,
∴AC平分∠DAB.
(2)解:由(1)得BF=DE,
∵CE=CF,CA=CA,
∴Rt△ACE≌Rt△ACF(HL),
∴AE=AF,
∴AB=AF﹣BF=AE﹣DE,
∵AE=6,DE=2,
∴AB=4.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目