题目内容
【题目】五一期间,小明随父母到某旅游胜地参观游览,他在游客中心O处测得景点A在其北偏东72°方向,测得景点B在其南偏东40°方向.小明从游客中心走了2千米到达景点A,已知景点B正好位于景点A的正南方向,求景点A与B之间的距离.(结果精确到0.1千米)
(参考数据:sin72°≈0.95,cos72°≈0.31,sin40°≈0.64,tan40°≈0.84)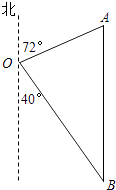
【答案】解:作OC⊥AB. 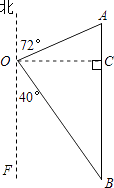
∵AB∥OF,
∴∠A=72°,∠B=40°,
∴在Rt△AOC中,
AC=2×cos72°≈2×0.31=0.62(千米),
OC=2×sin72°≈2×0.95=1.9(千米),
在Rt△BOC中,
![]() =tan40°,
=tan40°,
即 ![]() ≈0.84,
≈0.84,
BC≈ ![]() =2.26(千米),
=2.26(千米),
∴AB=0.62+2.26=2.88(千米).
【解析】首先过点O作OC⊥AB,垂足为C,然后在Rt△AOC中利用锐角三角函数的定义求出AC、OC的长,然后在Rt△OCB中,依据锐角三角函数的定义可求出BC的长,最后依据AB=AC+BC求解即可.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目