题目内容
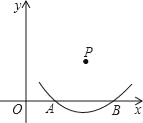
【题目】如图，在直角坐标系中，以点P为圆心的圆弧与x轴交于A、B两点，已知P（4，2）和A（2，0），则点B的坐标是_____．
【答案】（6，0）
【解析】连接PA、PB．过点P作PD⊥AB于点D．根据两点间的距离公式求得PA=2
；然后由已知条件“点P为圆心的圆弧与x轴交于A、B两点”知PA=PB=2
；再由垂径定理和勾股定理求得AD=1/2AB=2，所以AB=4，由两点间的距离公式知点B的坐标．
解：连接PA、PB．过点P作PD⊥AB于点D．
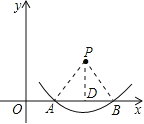
∵P（4，2）、A（2，0），
∴PA=
，PD=2；
∵点P为圆心的圆弧与x轴交于A、B两点，
∴PA=PB=2
，AB是垂直于直径的弦，
∴AD=DB；
在直角三角形PDA中，AD2=AP2-PD2，
∴AD=2；
∴AB=4，
∴B（6，0）．
故答案为：B（6，0）．
练习册系列答案
相关题目
【题目】由于雾霾天气频发，市场上防护口罩出现热销．某药店准备购进一批
两种不同型号口罩进行销售.下表是甲、乙两人购买两种型号口罩的情况：
A型号数量(单位：个) | B型号数量(单位：个) | 总售价(单位：元) | |
甲 | 1 | 3 | 26 |
乙 | 3 | 2 | 29 |
(1)求一个
型口罩和一个
型口罩的售价各是多少元？
(2)药店准备购进这两种型号的口罩共50个，其中型口罩数量不少于35个，且不多于型口罩的3倍，有几种购买方案？请写出购买方案.
(3)在(2)的条件下，药店在销售完这批口罩后，总售价能否达到282元？
