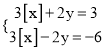题目内容
【题目】如图，已知点A从点（1，0）出发，以1个单位长度/秒的速度沿x轴向正方向运动，以O、A为顶点作菱形OABC，使点B、C在第一象限内，且∠AOC=60°，点P的坐标为（0，3），设点A运动了t秒，求：
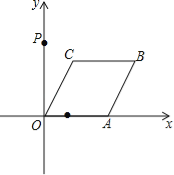
（1）点C的坐标（用含t的代数式表示）；
（2）点A在运动过程中，当t为何值时，使得△OCP为等腰三角形？
【答案】（1）点C的坐标为：（
（1+t），
（1+t））；（2）当t=
﹣1，t=2，t=3
﹣1时，均可使得△OCP为等腰三角形．
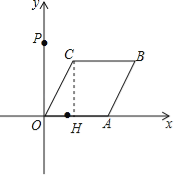
【解析】试题分析：（1）过点C作CH⊥x轴于点H，解直角三角形CHO，求出OH，CH的长，即可求出点C的坐标；
（2）因为等腰三角形OCP的腰和底不确定所以要分三种情况分别讨论：①当以O为等腰三角形顶点时；②当以C为等腰三角形顶点时；③当以P为等腰三角形顶点时，求出t的值即可．
解：（1）过点C作CH⊥x轴于点H，
根据题意得：OA=1+t，
∵四边形OABC是菱形，
∴OC=OA=1+t，
∵∠AOC=60°，
∴OH="OC"
cos60°=
OC=（1+t），CH="OC"sin60°=
（1+t），
∴点C的坐标为：（（1+t），（1+t））；
（2）①当以O为等腰三角形顶点时，OC=OP，
∴1+t=3，
∴t=2；
②当以C为等腰三角形顶点时，PC=OC，则CH=OP=
，
即
（1+t）=，
解得：t=
﹣1；
③当以P为等腰三角形顶点时，OP=PC，∠POC=30°，则Q（0，
），
∴OC=3，
∴1+t=3，
∴t=3﹣1，
综上可知，当t=﹣1，t=2，t=3
﹣1时，均可使得△OCP为等腰三角形．
【题目】某公司需招聘一名员工，对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核．甲、乙、丙各项得分如下表：
笔 试 | 面 试 | 体 能 | |
甲 | 85 | 80 | 75 |
乙 | 80 | 90 | 73 |
丙 | 83 | 79 | 90 |
（1）根据三项得分的平均分，从高到低确定三名应聘者的排名顺序．
（2）该公司规定：笔试，面试、体能得分分别不得低于80分，80分，70分，并按60%，30%，10%的比例计入总分（不计其他因素条件），请你说明谁将被录用．
