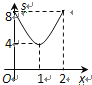
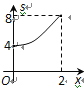
��Ŀ����
����Ŀ����ͼ�� l1��l2����1 = 105�㣬��2 = 140���������� = _____________��
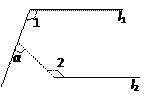
���𰸡�65��
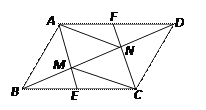
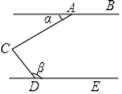
�������������������ӳ�CD��AE�ڵ�F������ƽ���ߵ����ʵõ�![]() ������������ǵ����ʵõ�
������������ǵ����ʵõ�![]() �������.
�������.
��⣺��ͼ�������ӳ�CD��AE�ڵ�F��
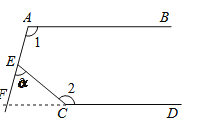
��AB��CD,![]()
��![]()
��![]()
��![]()
�ʴ�Ϊ��![]()
�㾦������ƽ���ߵ����ʺ���������ǵ����ʣ�����Ĺؼ�������������.
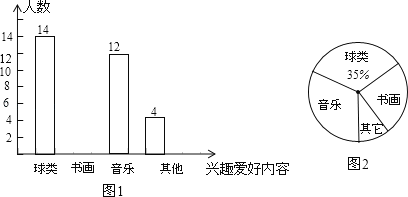
�����͡������
��������
14
����Ŀ����ͼ��AD����O��ֱ����AD=12����B��C����O�ϣ�AB��DC���ӳ��߽��ڵ�E����CB=CE����BCE=70��.
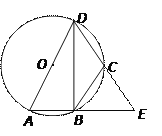
�����½��ۣ��١�ADE=��E�����ӻ�![]() �ij�Ϊ
�ij�Ϊ![]() ���۵�CΪ
���۵�CΪ![]() ���е㣻��BDƽ�֡�ADE.���Ͻ���һ����ȷ����_________________.������ȷ���۵���Ŷ����ϣ�
���е㣻��BDƽ�֡�ADE.���Ͻ���һ����ȷ����_________________.������ȷ���۵���Ŷ����ϣ�
���𰸡��٢ڢ�
���������������ٸ����ڽ��ı��εĶԽǻ����õ���CBE=��ADE�����ݵ��������ε����ʵõ���CBE=��E������֤��.
�����Բ�ĽǵĶ��������ݻ�����ʽ��⼴��.
��֤����DAC=��EAC������֤��.
�ܡ�A����E��BD��ƽ�֡�ADE.
��⣺�١�CBEΪԲ�ڽ��ı���ABCD����ǣ����CBE=��ADE��
CB=CE�����ԡ�CBE=��E����ˡ�ADE=��E.
�ڡ�A=��BCE=70�㣬���AOB=40�㣬![]() �ij�=
�ij�=![]()
��������֪��AC��DE���ɡ�ADE=��E��AD=AE��
���DAC=��EAC�����CΪ![]() ���е�.
���е�.
��DB��AE������A����E����BD��ƽ�֡�ADE. ��ȷ���ۢ٢ڢ�
�ʴ�Ϊ���٢ڢ�.