题目内容
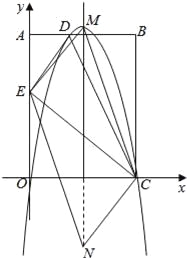
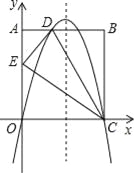
【题目】如图，在矩形OABC中，AO=10，AB=8，沿直线CD折叠矩形OABC的一边BC，使点B落在OA边上的点E处，分别以OC，OA所在的直线为x轴，y轴建立平面直角坐标系，抛物线y=ax2+bx+c经过O，D，C三点.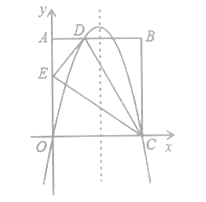
(1)求AD的长及抛物线的解析式；
(2)一动点P从点E出发，沿EC以每秒2个单位长的速度向点C运动，同时动点Q从点C出发，沿CO以每秒1个单位长的速度向点O运动，当点P运动到点C时，两点同时停止运动，设运动时间为t秒，当t为何值时，以P，Q，C为顶点的三角形与ADE相似？
(3)点N在抛物线对称轴上，点M在抛物线上，是否存在这样的点M与点N，使以M，N，C，E为顶点的四边形是平行四边形？若存在，请直接写出点M与点N的坐标（不写求解过程）；若不存在，请说明理由.
【答案】（1）y=﹣
x2+
x（2）t=
或
（3）①M1（4， 
），N1（4，﹣
）；②M2（12，﹣32），N2（4，﹣26）；③M3（﹣4，﹣32），N3（4，﹣38）．
【解析】试题分析：（1）根据折叠图形的轴对称性，△CED、△CBD全等，首先在Rt△CEO中求出OE的长，进而可得到AE的长；在Rt△AED中，AD=AB﹣BD、ED=BD，利用勾股定理可求出AD的长．进一步能确定D点坐标，利用待定系数法即可求出抛物线的解析式．
（2）由于∠DEC=90°，首先能确定的是∠AED=∠OCE，若以P、Q、C为顶点的三角形与△ADE相似，那么∠QPC=90°或∠PQC=90°，然后在这两种情况下，分别利用相似三角形的对应边成比例求出对应的t的值．
（3）由于以M，N，C，E为顶点的四边形，边和对角线都没明确指出，所以要分情况进行讨论：
①EC做平行四边形的对角线，那么EC、MN必互相平分，由于EC的中点正好在抛物线对称轴上，所以M点一定是抛物线的顶点；
②EC做平行四边形的边，那么EC、MN平行且相等，首先设出点N的坐标，然后结合E、C的横、纵坐标差表示出M点坐标，再将点M代入抛物线的解析式中，即可确定M、N的坐标．
试题解析：方法一：
解：（1）∵四边形ABCO为矩形，
∴∠OAB=∠AOC=∠B=90°，AB=CO=8，AO=BC=10．
由题意，△BDC≌△EDC．
∴∠B=∠DEC=90°，EC=BC=10，ED=BD．
由勾股定理易得EO=6．
∴AE=10﹣6=4，
设AD=x，则BD=ED=8﹣x，由勾股定理，得x2+42=（8﹣x）2，
解得，x=3，∴AD=3．
∵抛物线y=ax2+bx+c过点D（3，10），C（8，0），O（0，0）
∴
，
解得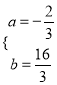
∴抛物线的解析式为：y=﹣
x2+
x．
（2）∵∠DEA+∠OEC=90°，∠OCE+∠OEC=90°，
∴∠DEA=∠OCE，
由（1）可得AD=3，AE=4，DE=5．
而CQ=t，EP=2t，∴PC=10﹣2t．
当∠PQC=∠DAE=90°，△ADE∽△QPC，
∴
，
即
，
解得t=
．
当∠QPC=∠DAE=90°，△ADE∽△PQC，
∴
，
即
，
解得t=
．
∴当t=
或
时，以P、Q、C为顶点的三角形与△ADE相似．
（3）假设存在符合条件的M、N点，分两种情况讨论：
①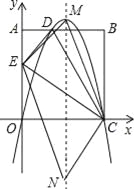
EC为平行四边形的对角线，由于抛物线的对称轴经过EC中点，若四边形MENC是平行四边形，那么M点必为抛物线顶点；
则：M（4， 
）；而平行四边形的对角线互相平分，那么线段MN必被EC中点（4，3）平分，则N（4，﹣
）；
②EC为平行四边形的边，则EC∥MN，EC=，MN设N（4，m），则M（4﹣8，m+6）或M（4+8，m﹣6）；
将M（﹣4，m+6）代入抛物线的解析式中，得：m=﹣38，此时 N（4，﹣38）、M（﹣4，﹣32）；
将M（12，m﹣6）代入抛物线的解析式中，得：m=﹣26，此时 N（4，﹣26）、M（12，﹣32）；
综上，存在符合条件的M、N点，且它们的坐标为：
①M1（﹣4，﹣32），N1（4，﹣38）；②M2（12，﹣32），N2（4，﹣26）；③M3（4， 
），N3（4，﹣
）．
