题目内容
【题目】某物流公司的快递车和货车同时从甲地出发，匀速向乙地行驶，快递车的速度为100km/h，货车的速度为60km/h，结果快递车比货车早2h到达乙地．快递车到达乙地后卸完物品再另装货物共用30min，立即按原路以90km/h速度匀速返回，直至与货车相遇．设两车之间的距离y（km）．货车行驶时间为x（h）．
（1）求甲、乙两地之间的距离．
（2）求快递车返回时y与x之间的函数关系式．
（3）建立适当的坐标系画出y与x之间的函数图象．
【答案】（1）300km；（2）y=﹣150x+615（3
≤x≤4
）．（3）见解析.
【解析】试题分析：（1）设甲、乙两地之间的距离为skm，根据时间=路程÷速度结合快递车比货车早2h到达乙地，即可得出关于s的一元一次方程，解之即可得出结论；
（2）先求出快递车离开乙地的时间以及此时两车间的距离，再根据路程=初始距离-两车速度和×行驶时间，即可得出快递车返回时y与x之间的函数关系式，找出x的取值范围，此题得解；
（3）找出当x=3时，y的值，由此可得出函数图象上的各节点坐标，描点、连线，即可画出函数图象．
解：（1）设甲、乙两地之间的距离为skm，
根据题意得：
﹣
=2，
解得：s=300．
答：甲、乙两地之间的距离为300km．
（2）快递车达到乙地的时间为300÷100=3（h），
快递车离开乙地的时间为3+
=3（h），
快递车离开乙地时，两车间的距离为300﹣60×3=90（km），
两车相遇的时间为3+90÷（60+90）=4
（h）．
∴快递车返回时y与x之间的函数关系式为y=90﹣（60+90）（x﹣3.5）=﹣150x+615（3≤x≤4
）．
（3）当x=3时，两车间的距离为300﹣60×3=120（km），
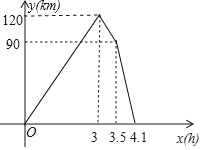
∴函数图象上各节点坐标为（0，0）、（3，120）、（3.5，90）、（4.1，0）．
画出函数图象，如图所示．
