Question

【题目】在梯形中，，点在直线上，联结，过点作的垂线，交直线与点，

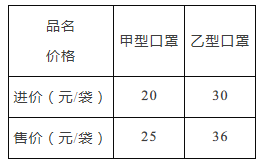
（1）如图1，已知，：求证：；

（2）已知：，

① 当点在线段上，求证：；

② 当点在射线上，①中的结论是否成立？如果成立，请写出证明过程；如果不成立，简述理由.

Answer 1

【答案】（1）证明见解析；

（2）①证明见解析；②结论仍然成立，证明见解析.

【解析】

（1）过F作FM⊥AD，交AD的延长线于点M，通过AAS证明△ABE≌△EMF，根据全等三角形的性质即可得出AB＝AD；

（2）①在AB上截取AG＝AE，连接EG．通过ASA证明△BGE≌△EDF，根据全等三角形的性质即可得出BE＝EF；

②

（1）如图：

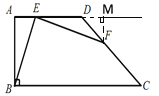
过F作FM⊥AD，交AD的延长线于点M，

∴∠M=90°，

∵∠BEF=90°，

∴∠AEB+MEF=90°，

∵∠A=90°，

∴∠ABE+∠AEB=90°，

∴∠MEF=∠ABE，

在△ABE和△EMF中，

，

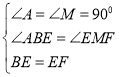∴△ABE≌△EMF(AAS)

∴AB=ME，AE=MF，

∵AM∥BC，∠C=45°，

∴∠MDF=∠C=45°，

∴∠DFM=45°，

∴DM=FM，

∴DM=AE，

∴DM+ED=AE+ED，

即AD=EM，

∴AB=AD；

（2）①证明：如图，

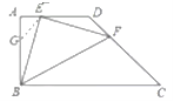
在AB上截取AG＝AE，连接EG，则∠AGE＝∠AEG，

∵∠A＝90°，∠A＋∠AGE＋∠AEG＝180°，

∴∠AGE＝45°，

∴∠BGE＝135°，

∵AD∥BC，

∴∠C＋∠D＝180°，

又∵∠C＝45°，

∴∠D＝135°，

∴∠BGE＝∠D，

∵AB＝AD，AG＝AE，

∴BG＝DE，

∵EF⊥BE，

∴∠BEF＝90°，

又∵∠A＋∠ABE＋∠AEB＝180°，

∠AEB＋∠BEF＋∠DEF＝180°，

∠A＝90°，

∴∠ABE＝∠DEF，

在△BGE与△EDF中，

，

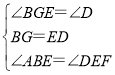∴△BGE≌△EDF（ASA），

∴BE＝EF；

②结论仍然成立，证明如下，

如图：

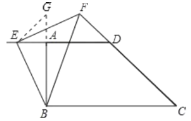
延长BA到点G，使BG=ED，连接EG，

则△EAG是等腰直角三角形，

∴∠EGB=45°，

∵ED∥BC，∠C=45°，

∴∠FDE=45°，

∴∠FDE=45°，

∴∠EGB=∠FDE，

∵∠A=90°，

∴∠AEB+∠ABE=90°，

∵EF⊥EB，

∴∠FED+∠AEB=90°，

∴∠AEB=∠FED，

在△BGE与△EFD中，

，

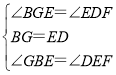∴△BGE≌△EDF（ASA），

∴BE＝EF.