题目内容
【题目】如图,抛物线的顶点坐标为C(0,8),并且经过A(8,0),点P是抛物线上点A,C间的一个动点(含端点),过点P作直线y=8的垂线,垂足为点F,点D,E的坐标分别为(0,6),(4,0),连接PD,PE,DE.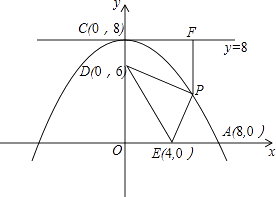
(1)求抛物线的解析式;
(2)猜想并探究:对于任意一点P,PD与PF的差是否为固定值?如果是,请求出此定值;如果不是,请说明理由;
(3)求:①当△PDE的周长最小时的点P坐标;②使△PDE的面积为整数的点P的个数.
【答案】
(1)解:设抛物线的解析式为y=ax2+8.
∵经过点A(8,0),
∴64a+8=0,解得a=﹣ ![]() .
.
抛物线的解析式为:y=﹣ ![]() x2+8
x2+8
(2)解:PD与PF的差是定值.
理由如下:设P(a,﹣ ![]() a2+8),则F(a,8),
a2+8),则F(a,8),
∵D(0,6),
∴PD= ![]() =
= ![]() =
= ![]() a2+2,PF=8﹣(
a2+2,PF=8﹣( ![]() )=
)= ![]() .
.
∴PD﹣PF=2.
(3)解:①当点P运动时,DE大小不变,则PE与PD的和最小时,△PDE的周长最小,
∵PD﹣PF=2,
∴PD=PF+2,
∴PE+PD=PE+PF+2,
∴当P、E、F三点共线时,PE+PF最小,此时点P,E的横坐标都为4,
∵将x=4代入y=﹣ ![]() x2+8,得y=6,
x2+8,得y=6,
∴P(4,6),此时△PDE的周长最小.
②如图1所示:过点P做PH⊥x轴,垂足为H.
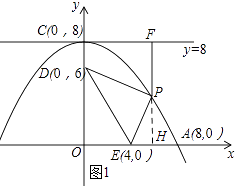
设P(a,﹣ ![]() a2+8)
a2+8)
∴PH=﹣ ![]() a2+8,EH=a﹣4,OH=a
a2+8,EH=a﹣4,OH=a
S△DPE=S梯形PHOD﹣S△PHE﹣S△DOE= ![]() a(﹣
a(﹣ ![]() a2+8+6)﹣
a2+8+6)﹣ ![]() (
( ![]() +8)(a﹣4)﹣
+8)(a﹣4)﹣ ![]() ×4×6=﹣
×4×6=﹣ ![]() a2+3a+4=﹣
a2+3a+4=﹣ ![]() (a﹣6)2+13.
(a﹣6)2+13.
∵点P是抛物线上点A,C间的一个动点(含端点),
∴0≤a≤8,
∴当a=6时,S△DPE取最大值为13.当a=0时,S△DPE取最小值为4.即4≤S△DPE≤13,其中,当S△DPE=12时,有两个点P.
∴共有11个令S△DPE为整数的点.
【解析】(1)此抛物线的顶点在y轴上,因此设此抛物线解析式为y=ax2+k,将点A、点B的坐标分别代入,就可求出函数解析式。
(2)抓住PF⊥直线y=8,设出点P、点F的坐标,用含a的代数式分别表示出PD、PF的长,再求出它们的差即可。
(3)①要使△PDE的周长最小,而DE的长是一个定值,关键是DP+PE的值要最小,由(2)可知PD=PF+2,即PE+PD=PE+PF+2,根据两点之间线段最短,P、E、F三点共线时,PE+PF最小,此时点P,E的横坐标都为4,代入函数解析式即可求出点P的坐标。②过点P做PH⊥x轴,垂足为H,设出点P的坐标,分别表示出PH、EH、的长,再求出S△DPE与a的函数关系式,根据点P是抛物线上点A,C间的一个动点(含端点),求出a的取值范围,继而求出S△DPE的取值范围,即可求出结果。
【考点精析】本题主要考查了二次函数的最值和勾股定理的概念的相关知识点,需要掌握如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题.

 阅读快车系列答案
阅读快车系列答案【题目】描点画图是探究未知函数图象变化规律的一个重要方法,下面是通过描点画图感知函数![]() 图象的变化规律的过程:
图象的变化规律的过程:
|
|
|
|
|
|
|
| … |
|
|
|
|
|
|
|
| … |
(1)如表是________与________的几组对应值,则:m=________;
(2)根据表中的数据,在平面直角坐标系![]() 中描出还未描出的点,并画出该函数的图象:
中描出还未描出的点,并画出该函数的图象:

(3)从函数图象可以看出,当________![]() 时,________随着________的增大而________(填增大或减小).
时,________随着________的增大而________(填增大或减小).







