题目内容
【题目】在平面直角坐标系中，O是坐标原点，ABCD的顶点A的坐标为（﹣2，0），点D的坐标为（0，2 
），点B在x轴的正半轴上，点E为线段AD的中点
（1）如图1，求∠DAO的大小及线段DE的长；
（2）过点E的直线l与x轴交于点F，与射线DC交于点G．连接OE，△OEF′是△OEF关于直线OE对称的图形，记直线EF′与射线DC的交点为H，△EHC的面积为3 ．
①如图2，当点G在点H的左侧时，求GH，DG的长；
②当点G在点H的右侧时，求点F的坐标（直接写出结果即可）．
【答案】
（1）解：∵A（﹣2，0），D（0，2 
）
∴AO=2，DO=2 ，
∴tan∠DAO= 
= ，
∴∠DAO=60°，
∴∠ADO=30°，
∴AD=2AO=4，
∵点E为线段AD中点，
∴DE=2；
（2）解：①如图2，
过点E作EM⊥CD，
∴CD∥AB，
∴∠EDM=∠DAB=60°，
∴EM=DEsin60°= ，
∴GH=6，
∵CD∥AB，
∴∠DGE=∠OFE，
∵△OEF′是△OEF关于直线OE的对称图形，
∴△OEF′≌△OEF，
∴∠OFE=∠OF′E，
∵点E是AD的中点，
∴OE= 
AD=AE，
∵∠EAO=60°，
∴△EAO是等边三角形，
∴∠EOA=60°，∠AEO=60°，
∵△OEF′≌△OEF，
∴∠EOF′=∠EOA=60°，
∴∠EOF′=∠AEO，
∴AD∥OF′，
∴∠OF′E=∠DEH，
∴∠DEH=∠DGE，
∵∠DEH=∠EDG，
∴△DHE∽△DEG，
∴ 
，
∴DE2=DG×DH，
设DG=x，则DH=x+6，
∴4=x（x+6），
∴x1=﹣3+ 
，x2=﹣3﹣ ，
∴DG=﹣3+ ．
②如图3，
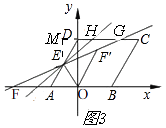
过点E作EM⊥CD，
∴CD∥AB，
∴∠EDM=∠DAB=60°，
∴EM=DEsin60°= ，
∴GH=6，
∵CD∥AB，
∴∠DHE=∠OFE，
∵△OEF′是△OEF关于直线OE的对称图形，
∴△OEF′≌△OEF，
∴∠OFE=∠OF′E，
∵点E是AD的中点，
∴OE= AD=AE，
∵∠EAO=60°，
∴△EAO是等边三角形，
∴∠EOA=60°，∠AEO=60°，
∵△OEF′≌△OEF，
∴∠EOF′=∠EOA=60°，
∴∠EOF′=∠AEO，
∴AD∥OF′，
∴∠OF′E=∠DEH，
∴∠DEG=∠DHE，
∵∠DEG=∠EDH，
∴△DGE∽△DEH，
∴ ，
∴DE2=DG×DH，
设DH=x，则DG=x+6，
∴4=x（x+6），
∴x1=﹣3+ ，x2=﹣3﹣ ，
∴DH=﹣3+ ．
∴DG=3+
∴DG=AF=3+ ，
∴OF=5+ ，
∴F（﹣5﹣ ，0）
【解析】（1）根据点A的坐，点D的坐标，在Rt△AOD中，利用解直角三角形易求出结论。
（2）①由（1）可知∠DAO=60°，添加辅助线，过点E作EM⊥CD，利用解直角三角形可求出EM、GH的长，根据已知易证明△OEF′≌△OEF，可得出角相等，点E是AD的中点，易得到△EAO是等边三角形，再证明△DHE∽△DEG，得出对应边成比例，设DG=x，则DH=x+6，建立方程，求出方程的解即可；②要求点F的坐标，就需求OF的长，解法与①类似求出DG，DG=AF，即可求出OF的长，从而求出点F的坐标。
【考点精析】通过灵活运用平行四边形的性质和相似三角形的判定与性质，掌握平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分；相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方即可以解答此题．
