题目内容
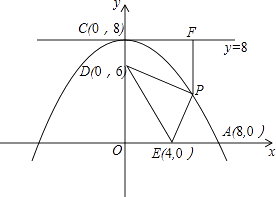
【题目】如图:在长方形ABCD中, AB=CD=4cm,BC=3cm,动点P从点A出发,先以1cm/s的速度沿A→B,然后以2cm/s的速度沿B→C运动,到C点停止运动,设点P运动的时间为t秒,是否存在这样的t,使得△BPD的面积S>3cm2?如果能,请求出t的取值范围;如果不能,请说明理由.

【答案】存在这样的t,使得△BPD的面积满足条件,此时0≤t<2;![]() <t≤5.5.
<t≤5.5.
【解析】
试题分两段考虑:①点P在AB上,②点P在BC上,分别用含t的式子表示出△BPD的面积,再由S>3cm2建立不等式,解出t的取值范围值即可.
试题解析:①当点P在AB上时,假设存在△BPD的面积满足条件,即运动时间为t秒,则
S△BPD=![]() (4-t)×3=
(4-t)×3=![]() (4-t)>3
(4-t)>3
解得t<2,
又因为P在AB上运动,0≤t≤4,
所以0≤t<2;
②当点P在BC上时,假设存在△BPD的面积满足条件,即运动时间为t秒,则
S△BPD=![]() (4-t)×2×4=4t-16>3
(4-t)×2×4=4t-16>3
解得t>![]() ,
,
又因为P在BC上运动,4<t≤5.5,
所以![]() <t≤5.5;
<t≤5.5;
综上所知,存在这样的t,使得△BPD的面积满足条件,此时0≤t<2;![]() <t≤5.5.
<t≤5.5.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
【题目】铁一课间餐种类繁多,深受学生喜爱.这天饭堂在课间的出品有鸡腿、薯饼、鱼丸和鸡柳.某同学就九年级学生对课间餐各类食物的喜爱程度做了抽样调查,制成表格如下:
课间餐种类 | 人类 | 百分比 |
鸡腿 | 150 | 60% |
薯饼 | 30 | a |
鱼丸 | b | 12% |
鸡柳 | 40 | c |
(1)样本容量是 , a= , b= , c= .
(2)若小王和小李商议着一起去买课间餐,若他们对以上四种口味的课间餐喜爱程度相同.请你帮他们算一算他们买了相同课间餐的概率.