Question

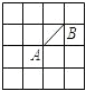
【题目】如图，在Rt△ABC中，∠ACB＝90°，AC＝3，BC＝4，点D在AB上，AD＝AC，AF⊥CD交CD于点E，交CB于点F，则CF的长是（　）

A.1.5B.1.8C.2D.2.5

Answer 1

【答案】A

【解析】

连接DF，由勾股定理求出AB=5，由等腰三角形的性质得出CE=DE，由线段垂直平分线的性质得出CF=DF，由SSS证明△ADF≌△ACF，得出∠ADF=∠ACF=∠BDF=90°，设CF=DF=x，则BF=4-x，在Rt△BDF中，由勾股定理得出方程，解方程即可．

解：连接DF，如图所示：

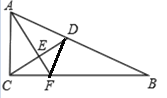
∵在Rt△ABC中，∠ACB=90°，AC=3，BC=4，

∴

∵AD=AC=3，AF⊥CD，

∴CE=DE，BD=AB-AD=2，∴CF=DF，

在△ADF和△ACF中，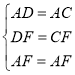

∴△ADF≌△ACF（SSS），

∴∠ADF=∠ACF=90°，

∴∠BDF=90°，

设CF=DF=x，则BF=4-x，

在Rt△BDF中，由勾股定理得: ，

即，

解得：x=1.5；

∴CF=1.5；

故选：A．