题目内容
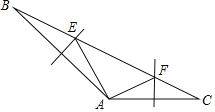
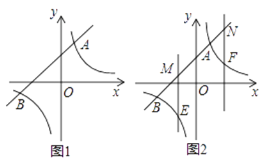
【题目】如图1所示,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交A(1,4),B(-4,c)两点,
的图象交A(1,4),B(-4,c)两点,
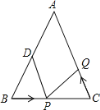
如图2所示,点M、N都在直线AB上,过M、N分别作y轴的平行线交双曲线于E、F,设M、N的横坐标分别为m、n,且 4 < m < 0 , n > 1 ,请探究,当m、n满足什么关系时,ME=NE.
(1)求反比例函数及一次函数的解析式;
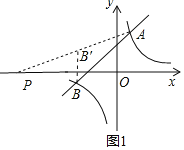
(2)点P是x轴上一动点,使|PA-PB|的值最大,求点P的坐标及△PAB的面积;
(3)如图2所示,点M、N都在直线AB上,过M、N分别作y轴的平行线交双曲线于E、F,设M、N的横坐标分别为m、n,且 ![]() , n>1,请探究,当m、n满足什么关系时,ME=NE.
, n>1,请探究,当m、n满足什么关系时,ME=NE.
【答案】(1) y= ![]() ,y=x+3.;(2) P点坐标为(-
,y=x+3.;(2) P点坐标为(- ![]() ,0),S△PAB=
,0),S△PAB= ![]() ;(3)见解析.
;(3)见解析.
【解析】(1)利用待定系数法即可解决问题;
(2)作B关于x轴的对称点B′(-4,1),连接AB′并延长交x轴于P,此时|PA-PB|的值最大,求出直线AB′的解析式即可解决问题;
(3)由题意可知,M(m,m+3),N(n,n+3),E(m,![]() ),F(n,
),F(n,![]() ),根据ME=NF,可得m+3-
),根据ME=NF,可得m+3-![]() =n+3-
=n+3-![]() ,即(m-n)(1+
,即(m-n)(1+![]() )=0,由此即可解决问题;
)=0,由此即可解决问题;
(1)把A(1,4)代入y=![]() ,可得a=4,
,可得a=4,
∴反比例函数的解析式为y=![]() ,
,
把B(-4,c)代入y=![]() ,得到c=-1,
,得到c=-1,
∴B(-4,-1),
把A(1,4),B(-4,-1)代入y=kx+b
得到![]() ,解得
,解得![]() ,
,
∴一次函数的解析式为y=x+3.
(2)作B关于x轴的对称点B′(-4,1),连接AB′并延长交x轴于P,此时|PA-PB|的值最大,
设AB′的解析式为y=k′x+b′,则有![]() ,
,
解得 ,
,
∴直线AB′的解析式为y=![]() x+
x+![]() ,
,
令y=0,得到x=-![]() ,
,
∴P(-![]() ,0),
,0),
∴S△PAB=![]() ×
×![]() ×(4+1)=
×(4+1)=![]() .
.
(3)如图2中,
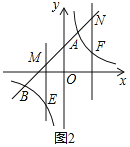
由题意可知,M(m,m+3),N(n,n+3),E(m,![]() ),F(n,
),F(n,![]() ),
),
∵-4<m<0,n>1,
∴ME=m+3-![]() ,NF=n+3-
,NF=n+3-![]() ,
,
当ME=NF时,m+3-![]() =n+3-
=n+3-![]() ,
,
即(m-n)(1+![]() )=0,
)=0,
∵-4<m<0,n>1,
∴m≠n,1+![]() =0,
=0,
∴mn=-4,
∴当mn=-4时,ME=NF.

【题目】 某校七年级共有男生63名,为了参加全校运动会,七年级准备从本年级所有男生中挑选出身高相差不多的40名男生组成仪仗队,为此,收集到所有男生的身高数据(单位:cm),经过整理获得如下信息:
a.小明把所有男生的身高数据按由低到高整理为如下,但因为不小心有部分数据被墨迹遮挡:

b.小刚绘制了七年级所有男生身高的频数分布表
身高分组 | 划记 | 频数 |
149≤x<152 | 丅 | 2 |
152≤x<155 | 正一 | 6 |
155≤x<158 | 正正丅 | 12 |
158≤x<161 | 正正正 | 19 |
161≤x<164 | 正正 | 10 |
164≤x<167 | ______ | ______ |
167≤x<170 | ______ | ______ |
170≤x<173 | 丅 | 2 |
c.该校七年级男生身高的平均数、中位数、众数如下:
平均数 | 中位数 | 众数 |
160 | m | n |
根据以上信息,回答下列问题:
(1)补全b表中频数分布表;
(2)直接写出c表中m,n的值;
(3)借助于已给信息,确定挑选出参加仪仗队的男生的身高范围;
(4)若本区七年级共有男生1260名,利用以上数据估计,全区七年级男生身高达到160及以上的男生约有多少人?