题目内容
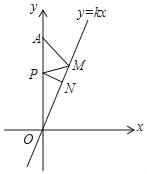
【题目】如图，已知正比例函数y=kx（k＞0）的图象与x轴相交所成的锐角为70°，定点A的坐标为（0，8），P为y轴上的一个动点，M、N为函数y=kx（k＞0）的图象上的两个动点，则AM+MP+PN的最小值为（ ）
A. 4 B. 4
C. 8sin40° D. 8sin20°（1+cos20°+sin20°cos20°）
【答案】B
【解析】
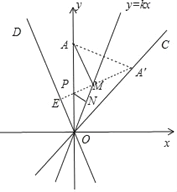
作y轴关于直线y=kx对称的对称直线OC，作直线y=kx关于y轴对称的对称直线OD，点A′是点A关于直线y=kx的对称点．作A′E⊥OD垂足为E，交y轴于点P，交直线y=kx于M，作PN⊥直线y=kx垂足为N，如图，
∵PN=PE，AM=A′M，
∴AM+PM+PN=A′M+PM+PE=A′E，
∴此时AM+MP+PN值最小，
在Rt△A′EO中，∵∠A′EO=90°，OA′=OA=8，∠A′OE=3∠AOM=60°，
∴OE=
OA′=4，
∴A′E=
OE=4，
即AM+MP+PN的最小值为4．
故选：B．
练习册系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
