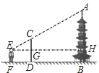
题目内容
【题目】如图,为了测量出楼房AC的高度,从距离楼底C处![]() 米的点D(点D与楼底C在同一水平面上)出发,沿斜面坡度为i=1:
米的点D(点D与楼底C在同一水平面上)出发,沿斜面坡度为i=1:![]() 的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈
的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈![]() ,计算结果用根号表示,不取近似值).
,计算结果用根号表示,不取近似值).

【答案】![]() .
.
【解析】
如图作BN⊥CD于N,BM⊥AC于M,先在RT△BDN中求出线段BN,在RT△ABM中求出AM,再证明四边形CMBN是矩形,得CM=BN即可解决问题.
如图作BN⊥CD于N,BM⊥AC于M.
在RT△BDN中,
BD=30,BN:ND=1:![]() ,
,
∴BN=15,DN=![]() ,
,
∵∠C=∠CMB=∠CNB=90°,
∴四边形CMBN是矩形,
∴CM=BM=15,BM=CN=![]() ,
,
在RT△ABM中,tan∠ABM=![]() ,
,
∴AM=![]() ,
,
∴AC=AM+CM=![]() .
.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目