题目内容
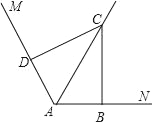
【题目】(题文)如图![]() ,在平面直角坐标系
,在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 经过点
经过点![]() ,顶点为点
,顶点为点![]() ,点
,点![]() 为抛物线上的一个动点,
为抛物线上的一个动点,![]() 是过点
是过点![]() 且垂直于
且垂直于![]() 轴的直线,过
轴的直线,过![]() 作
作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() .
.
![]() 求抛物线的解析式,并写出其顶点
求抛物线的解析式,并写出其顶点![]() 的坐标;
的坐标;
![]() ①当
①当![]() 点运动到
点运动到![]() 点处时,计算:
点处时,计算:![]() ________,
________,![]() ________,由此发现,
________,由此发现,![]() ________
________![]() (填“
(填“![]() ”、“
”、“![]() ”或“
”或“![]() ”);
”);
②当![]() 点在抛物线上运动时,猜想
点在抛物线上运动时,猜想![]() 与
与![]() 有什么数量关系,并证明你的猜想;
有什么数量关系,并证明你的猜想;
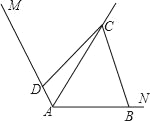
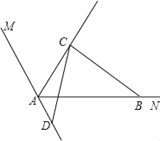
![]() 如图
如图![]() ,设点
,设点![]() ,问是否存在点
,问是否存在点![]() ,使得以
,使得以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?若存在,求出
相似?若存在,求出![]() 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.


【答案】55=
【解析】
对于(1)用待定系数法,将A点坐标代入![]() 可得出a的值,而顶点B是在x=
可得出a的值,而顶点B是在x=![]() 即x=0,可求出B点坐标;
即x=0,可求出B点坐标;
对于(2)可以直接根据图像和已知条件,求出PO和PH的值,然后根据所求出的值,来判断是否相等.
对于(3)可以先假设是存在的,然后已知条件就是以点O,O,H为顶点的三角形与△ABC相似,以此为已知条件,推出P点的坐标,看是否能推出P点,成功则存在,反之则不存在.
![]() 解:∵抛物线
解:∵抛物线![]() 经过点
经过点![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴抛物线解析式为![]() ,顶点
,顶点![]() .
.
![]() ①当
①当![]() 点运动到
点运动到![]() 点处时,∵
点处时,∵![]() ,
,![]() ,
,
∴![]() ,
,
![]() ∵
∵![]() ,
,![]() ,
,![]()
∴![]() ,
,
∵![]() ,
,
又∵以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似,
相似,
∴![]() 与
与![]() ,
,![]() 与
与![]() 是对应边,
是对应边,
∴![]() ,设点
,设点![]() ,
,
∴![]() ,
,
解得![]() ,
,
∴点![]() 坐标
坐标![]() 或
或![]() .
.

练习册系列答案
相关题目