Question

【题目】如图，在四边形ABCD中，∠ABC=90°，AB=3，BC=4，CD=5，DA=，则BD的长为__________.

Answer 1

【答案】．

【解析】

作DM⊥BC，交BC延长线于M，由勾股定理得出AC2=AB2+BC2=25，求出AC2+CD2=AD2，由勾股定理的逆定理得出△ACD是直角三角形，∠ACD=90°，证出∠ACB=∠CDM，得出△ABC≌△CMD，由全等三角形的性质求出CM=AB=3，DM=BC=4，得出BM=BC+CM=7，再由勾股定理求出BD即可．

作DM⊥BC，交BC延长线于M，如图所示：

则∠M=90°，
∴∠DCM+∠CDM=90°，
∵∠ABC=90°，AB=3，BC=4，
∴AC2=AB2+BC2=25，
∴AC=5，
∵AD=，CD=5，
∴AC2+CD2=AD2，
∴△ACD是直角三角形，∠ACD=90°，
∴∠ACB+∠DCM=90°，
∴∠ACB=∠CDM，
∵∠ABC=∠M=90°，
在△ABC和△CMD中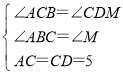
，
∴△ABC≌△CMD，
∴CM=AB=3，DM=BC=4，
∴BM=BC+CM=7，
∴BD=，
故答案为：．