��Ŀ����
����Ŀ��ͨ��ѧϰ���Ǻ���������֪����ֱ���������У�һ����ǵĴ�С�������߳��ı�ֵ�Ψһȷ������˱߳���ǵĴ�С֮������ת��.���Ƶģ������ڵ����������н����߽�֮�����ϵ.���Ƕ��壺�����������еױ������ıȽ������ǵ�����(sad).��ͼ1���ڡ�ABC�У�AB��AC������A�����Լ���sadA����ʱsadA��![]() .����֪��һ���ǵĴ�С������ǵ�����ֵҲ���Ψһȷ����.���������ǵ����Զ��壬����������⣺
.����֪��һ���ǵĴ�С������ǵ�����ֵҲ���Ψһȷ����.���������ǵ����Զ��壬����������⣺

(1)sad60�㣽 ��
(2)����0�㣼��A��180�㣬��A������ֵsadA��ȡֵ��Χ�� ��
(3)��ͼ�ڣ���֪sinA��![]() �����С�AΪ��ǣ�����sadA��ֵ.
�����С�AΪ��ǣ�����sadA��ֵ.
���𰸡�(1)1;(2) 0<sadA<2; (3) ![]() .
.
��������
��1���������⣬�ж�������Ϊ�ȱ������Σ�Ȼ��������ԵĶ�����
��2�����0���180��ʱ���������ε����ıȼ��ɣ�
��3����ͼ����AB��ȡAD��AC������D��DE��AC�ڵ�E������CD����AB��5a��BC��3a����AC��4a��Ȼ�����CD�ij����ٸ������ԵĶ�����.
�⣺(1)���������֪��������Ϊ60��ʱ�����������ε�ҲΪ60�㣬
���������Ϊ�ȱ������Σ�
��sad60�㣽1��
�ʴ�Ϊ1��
(2)����A�ӽ�0��ʱ��sadA�ӽ�0��
����A�ӽ�180��ʱ�����������εĵӽ������Ķ�������sadA�ӽ�2��
��sadA��ȡֵ��ΧΪ��0<sadA<2��
(3) 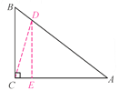 ��AB��5a��BC��3a����AC��4a��
��AB��5a��BC��3a����AC��4a��
��ͼ����AB��ȡAD��AC��4a������D��DE��AC�ڵ�E������CD��
��DE��AD��sinA��4a��![]() ��
��![]() a��AE��AD��cosA��4a��
a��AE��AD��cosA��4a��![]() ��
��![]() a��
a��
��CE��4a��![]() a��
a��![]() a��
a��
����Rt��DCE��
CD��![]() ��
��![]() ��
��![]() a��
a��
��sadA��![]() ��
��![]() .
.

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�




